Rotational Raman selection rules for symmetric rotors

Rotational Raman selection rules for symmetric rotors describe the allowed changes in a symmetric top’s rotational angular momentum states during inelastic light scattering.

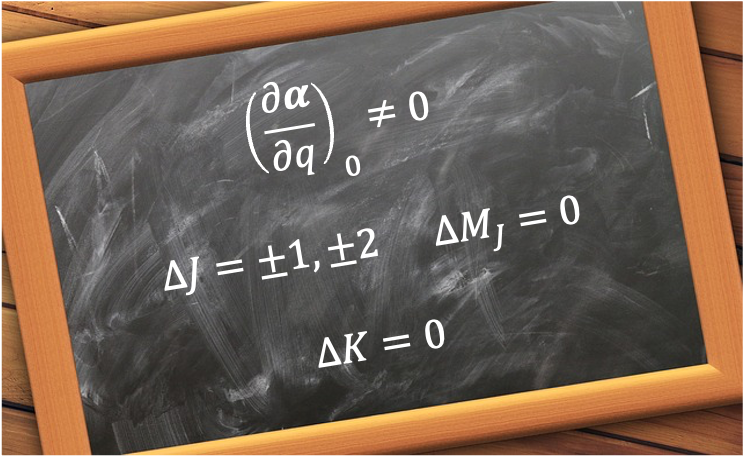
A symmetry rotor, such as CH₃Cl, has a permanent electric dipole moment along its symmetry axis. At finite temperatures, the total angular momentum $\boldsymbol{\mathit{J}}$ of the rotating molecule is generally not parallel to the symmetry axis and given by:

$\boldsymbol{\mathit{J}}=I_{\parallel}\omega_{\parallel}\hat{e}_3+I_{\perp}\boldsymbol{\mathit{\omega}}_{\perp}$

where $\hat{e}_3$ is the unit vector along the symmetry axis.

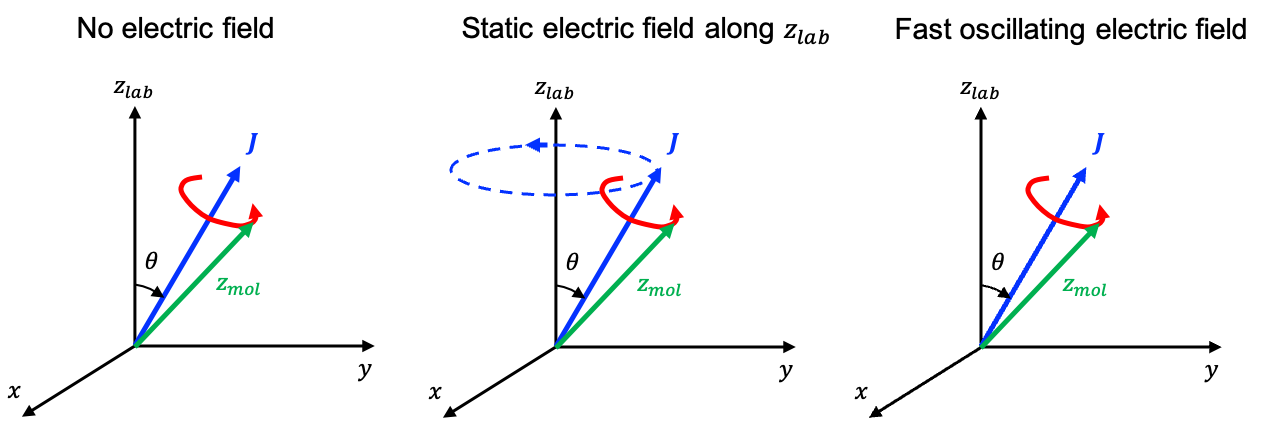
In the absence of external interactions (e.g. an electric field), the vector $\boldsymbol{\mathit{J}}$ is conserved. This is because space is isotropic and the physics is unchanged regardless of the orientation of the molecule. It follows that the symmetry axis of the molecule must precess around $\boldsymbol{\mathit{J}}$ so that its projection onto $\boldsymbol{\mathit{J}}$ stays constant as the molecule rotates (see diagram below).

Question

Why must the projection of the symmetry axis of the molecule onto $\boldsymbol{\mathit{J}}$ remain constant as the molecule rotates?

Answer

The rotational energy of the molecule is given by:

$E=\frac{J_{\perp}^2}{2I_{\perp}}+\frac{J_{\parallel}^2}{2I_{\parallel}}$

where $J_{\parallel}=\boldsymbol{\mathit{J}}\cdot\hat{e}_3$ is the projection of $\boldsymbol{\mathit{J}}$ onto the symmetry axis.

Substituting $J_{\perp}^2=J^2-J_{\parallel}^2$ into $E$ gives:

$E=\frac{J_{\perp}^2}{2I_{\perp}}+J_{\parallel}^2\biggr$\frac{1}{2J_{\parallel}}-\frac{1}{2I_{\perp}}\biggr$$

For a given $E$ , $J^2$ is conserved, and the two moments of inertia are also constant. Therefore, $J_{\parallel}=\boldsymbol{\mathit{J}}\cdot\hat{e}_3$ must be a constant. Since, the projection of $\boldsymbol{\mathit{J}}$ onto the symmetry axis and the projection of the symmetry axis onto $\boldsymbol{\mathit{J}}$ are related by the same constant angle, the projection of the symmetry axis of the molecule onto $\boldsymbol{\mathit{J}}$ remains constant as the molecule rotates.

In the presence of a static electric field, the interaction of the field with the molecule’s dipole moment generates a torque on the molecule given by

$\boldsymbol{\mathit{\tau}}=\boldsymbol{\mathit{\mu}}\times\boldsymbol{\mathit{E}}=\mu Esin\theta$

where $\theta$ is the angle between $\boldsymbol{\mathit{\mu}}$ and $\boldsymbol{\mathit{E}}$ .

This torque changes the molecule’s angular momentum vector according to

$\frac{d\boldsymbol{\mathit{J}}}{dt}=\boldsymbol{\mathit{\tau}}$

Because the torque is perpendicular to the electric field direction (taken as the lab $z$ -axis), its component along the field axis is zero. Consequently, the projection $J_z$ of $\boldsymbol{\mathit{J}}$ onto that axis cannot change. The only way for $\boldsymbol{\mathit{J}}$ to change over time, while keeping a constant projection onto the lab $z$ -axis is for it to precess around the direction of the electric field.

As a result, the molecular axis undergoes a compound motion with a fast precession around $\boldsymbol{\mathit{J}}$ and a slower precession of $\boldsymbol{\mathit{J}}$ around the static electric field line (see above diagram). However, in Raman spectroscopy, the laser produces an electric field that oscillates at about 10¹⁴ to 10¹⁵ Hz, which is much faster than the molecule can physically rotate or precess. The interaction between the field and the molecule’s permanent dipole averages to zero, resulting in no net torque on the permanent dipole and hence no precession of $\boldsymbol{\mathit{J}}$ around the electric field line.

While the permanent dipole interaction averages to zero, the induced dipole interaction does not, because it is not confined to the molecular axis. Nevertheless, the interaction between the induced dipole and the electric field is typically very weak, leaving the precession of the molecular axis around $\boldsymbol{\mathit{J}}$ as the dominant motion.

In the molecular frame, the polarisability tensor of a symmetric rotor is mathematically identical to that of a linear molecule. This because both linear rotors and symmetric rotors possess cylindrical symmetry (or higher) about their principal axis. It follows that the projection of the molecular induced dipole moment onto the direction of the electric field (laboratory $z$ -axis) is given by eq7a, or equivalently,

$\alpha=\alpha_{\perp}+\Delta\alpha cos^2\theta\;\;\;\;\;\;\;\;20$

where $\Delta\alpha=\alpha_{\parallel}-\alpha_{\perp}$ .

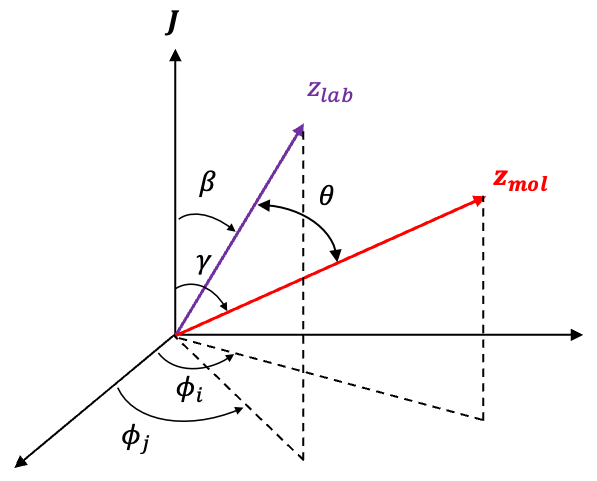
Substituting the spherical law of cosines (see diagram above), where $cos\theta=cos\beta cos\gamma+sin\beta sin\gamma cos\omega_rt$ into eq20 gives:

$\alpha=\alpha_{\perp}+\Delta\alpha(cos\beta cos\gamma+sin\beta sin\gamma cos\omega_rt)^2$

Expanding the equation and using the identity $cos^2\omega_rt=\frac{1}{2}(1+cos2\omega_rt)$ yields:

$\alpha=\alpha_{0}+Acos\omega_rt+Bcos2\omega_rt\;\;\;\;\;\;\;\;21$

where

$\alpha_{0}=\alpha_{\perp}+\Delta\alpha\biggr$cos^2\beta cos^2\gamma+\frac{1}{2}sin^2\beta sin^2\gamma\biggr$$
$A=\Delta\alpha(2cos\beta cos\gamma sin\beta sin\gamma)$
$B=\frac{\Delta\alpha}{2}sin^2\beta sin^2\gamma$

The selection rules involving the quantum number $J$ can be explained semiclassically, with the induced dipole moment given by:

$\mu_{ind}=\alpha Ecos\omega_it\;\;\;\;\;\;\;\;22$

where $\omega_i$ is the angular frequency of the incident radiation.

Substituting eq21 into eq22 results in:

$\mu_{ind}=\alpha_0 Ecos\omega_it+AEcos\omega_itcos\omega_rt+BEcos\omega_itcos2\omega_rt$

Using the identity $cosxcosy=\frac{1}{2}[cos(x+y)+cos(x-y)]$ gives:

$\begin{align}\mu_{ind}=&\alpha_0 Ecos\omega_it+\frac{AE}{2}[cos(\omega_i+\omega_r)t+cos(\omega_i-\omega_r)t]\\&+\frac{BE}{2}[cos(\omega_i+2\omega_r)t+cos(\omega_i-2\omega_r)t]\;\;\;\;\;\;\;\;23\end{align}$

This equation shows that the induced dipole moment consists of five components: one oscillating at the incident frequency, two at $\omega_i\pm\omega_r$ , and two at $\omega_i\pm 2\omega_r$ . Each time-dependent component of the induced dipole moment corresponds to an oscillating dipole, which radiates electromagnetic energy at the frequency at which it oscillates. It follows that the component oscillating at $\omega_i$ gives rise to Rayleigh-scattered radiation, while those at $\omega_i\pm\omega_r$ and $\omega_i\pm 2\omega_r$ produce Raman-scattered radiation.

Question

Why does each component on the RHS of eq23 correspond to an oscillating, rather than the entire sum corresponding to a single oscillating dipole?

Answer

An oscillating electric dipole is defined by a dipole moment that varies sinusoidally in time at a single frequency, for example $\mu=\mu_0cos\omega t$ . Therefore, eq23 represents a superposition of five independent sinusoidal components, which can be viewed as a Fourier decomposition of the induced dipole moment. Each term oscillates at a distinct frequency and therefore corresponds to an independent oscillating dipole that radiates at that frequency.

Raman selection rules are often discussed for thermally populated rotational levels, where $J$ is typically large (the classical limit). For large $J$ , the magnitude of the quantum angular momentum of the molecule is $L=\hbar\sqrt{J(J+1)}\approx \hbar J$ . Substituting this approximation into $L=I\omega_r$ gives:

$\omega_r\approx\frac{\hbar J}{I}$

$\omega_i-\omega_r$ is the angular frequency of a Stokes-scattered photon, which is associated with the resultant quantum rotational transitional frequency of $\omega_i-(\omega_i-\omega_r)=+\omega_r\approx\frac{\hbar J}{I}$ . This corresponds to the selection rule $\Delta J=+1$ , because at large $J$ ,

$\begin{align}\Delta E&=E_{J+1}-E_J=\frac{\hbar^2}{2I}[(J+1)(J+2)-J(J+1)]\\&=\frac{\hbar^2}{2I}(2J+1)\approx\frac{\hbar^2J}{I}\end{align}$

Similarly, the angular frequency $\omega_i+\omega_r$ (anti-Stokes scattering) leads to the selection rule $\Delta J=-1$ , while $\omega_i\mp 2\omega_r$ corresponds to $\Delta J=\pm 2$ . For the selection rules involving the remaining quantum numbers $M_J$ and $K$ , we refer to the time-dependent perturbation theory, which states that the transition probability $\vert T\vert^2$ can be found by evaluating:

$T=\int_0^{\pi}\int_0^{2\pi}\int_0^{2\pi}\psi^*_{J^{'}K^{'}M^{'}_J}\mu_{ind}\psi_{JKM_J}sin\theta d\theta d\phi d\chi$

where $\psi^*_{J^{'}K^{'}M^{'}_J}=d^{J^{'}}_{M_J^{'}K^{'}}(\theta)e^{iM^{'}_J\phi}e^{iK^{'}\chi}$ and $\psi_{JKM_J}=d^{J}_{M_JK}(\theta)e^{-iM_J\phi}e^{-iK\chi}$ are the Wigner D-functions.

The integrals $\int_0^{2\pi}e^{i(M^{'}_J-M_J)\phi}d\phi$ and $\int_0^{2\pi}e^{i(K^{'}-K)\chi}d\chi$ are non-zero only if $M_J=M_J^{'}$ and $K=K'$ . This confirms that we require $\Delta M_J=0$ and $\Delta K=0$ for a probable transition to occur ( $T\neq 0$ ).