The ideal gas law is derived from the statistical thermodynamic expression for pressure using the canonical partition function of non-interacting, indistinguishable particles.
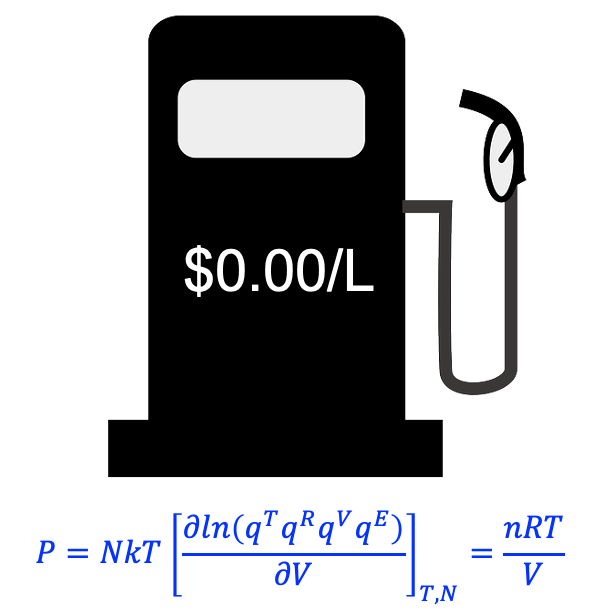
Substituting eq257 into eq322 gives:
Since only the translational molecular partition function is dependent on
, we have
Substituting eq266 into eq350 yields:
With , where
is the Avogadro constant and
is the number of moles, we have the ideal gas law:
where the universal gas constant .
This derivation demonstrates how macroscopic thermodynamic laws are consistent with the microscopic principles of quantum mechanics, as described by statistical thermodynamics. It reinforces the concept that, in an ideal gas, the particles are non-interacting point masses whose energy is solely due to translational motion.