The rigid rotor is a fundamental model in quantum mechanics used to describe the rotational motion of a molecule, particularly diatomic molecules, where the two atoms are treated as point masses connected by a fixed-length bond. This simplification assumes that the molecule does not vibrate or stretch during rotation, allowing the system to be treated as a rigid body rotating in space. The model works reasonably well in the microwave frequency range of 1011 to 1012 Hz and provides critical insights into energy levels associated with molecular rotation.
For the more general case of a diatomic molecule’s internal motion (encompassing both rotational and vibrational motions), the Schrödinger equation for the two particles, can be derived by reducing the two-particle problem to a one-particle problem. The result is given by eq311:
where
is the kinetic energy operator of the internal motion of the system,
is the reduced mass of the molecule,
is the internuclear potential energy ,
is the molecular wavefunction in spherical coordinates,
is the eigenvalue corresponding to the wavefunction.
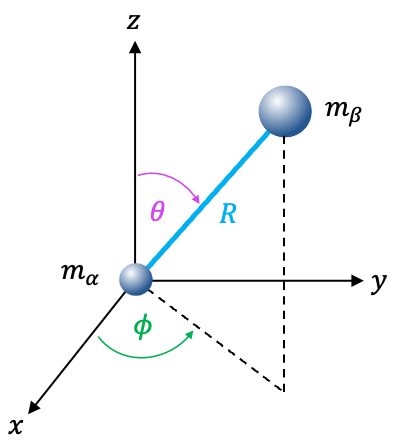
Within the rigid rotor approximation, the bond length is fixed ( is a constant) and
. The above equation simplifies to a rotational Schrödinger equation:
Eq1 is equivalent to a Schrödinger equation for a particle of mass constrained to a spherical surface of zero relative potential and radius
. The eigenfunctions of this system are the spherical harmonics
, and the Hamiltonian can be explicitly written as (see eq50 of an eariler article):
Here, is the moment of inertia and
is the square of the angular momentum operator, with eigenvalues (see eq133):
Replacing with
, the rotational quantum number, the energy of the rigid rotor is:

Question
The eigenvalue equation is associated with the angular momentum eigenvalue of an electron rotating about an origin. Is it also applicable to a nucleus rotating around a point?
Answer
Yes. This is because the spherical harmonics are general solutions to the angular part of the Schrödinger equation and describe the angular momentum states of a rotating particle. These states can represent either an electron or a nucleus rotating about a point, depending on the system being modelled.
Eq3 can also be derived from classical mechanics, where the rotational kinetic energy of a particle with reduced mass is
with and
, where
is the magnitude of the angular velocity vector
.
Substituting the classical angular momentum into eq4 yields
Using the quantum mechanics postulate that “to every observable quantity in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics”, and replacing the classical angular momentum with the quantum mechanical operator gives
which is equivalent to eq2, and hence allows us to derive eq3.
The same postulate also enables us to derive similar energy expressions for polyatomic molecules. However, we must first examine the different moments of inertia for some common classes of polyatomic molecules, and to do that, we need to understand the parallel axis theorem.

Question
How many axes of rotation does a diatomic molecule have? If it has more than one, why is there only one moment of inertia mathematical expression ?
Answer
A diatomic molecule has three principal axes of rotation that pass through its centre of mass and are mutually perpendicular, just like any rigid body. However, since the molecule is linear, the axis aligned with the bond (commonly taken as the z-axis) passes through both atoms, meaning the mass has no perpendicular displacement from this axis. As a result, the moment of inertia about this axis is zero: .
The other two axes, both perpendicular to the bond, are physically equivalent due to the molecule’s cylindrical symmetry. Rotation about either of these axes produces the same resistance to rotation, leading to equal moments of inertia: . Therefore, although the molecule has three rotational axes, only one unique, nonzero moment of inertia expression is needed.
In other words, different axes of rotation will have different moments of inertia. In general, for a rigid body rotating in 3D space, the moment of inertia can be conveniently expressed as the following matrix, called the inertia tensor:
with
where ,
and
.
Eq4b states that , which is consistent with classical mechanics (see this article). It follows that:

Question
Why is , and not
or
?
Answer
is a scalar, and only
evaluates to a scalar. The other two expressions result in matrices and are not valid for representing energy.
Substituting ,
and
back into eq4c gives
and hence