Thermodynamic functions involving the canonical partition function describe thermodynamic properties of a canonical ensemble.
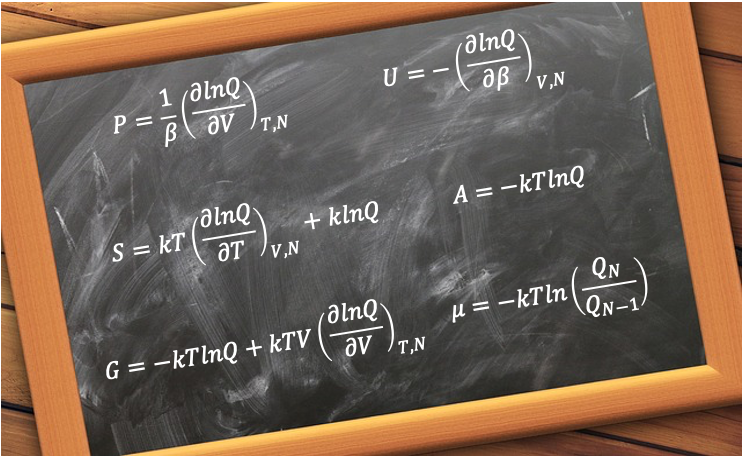
In statistical mechanics, the canonical ensemble provides a powerful framework for connecting microscopic states to macroscopic thermodynamic properties. Central to this approach is the canonical partition function, 
, which encapsulates the statistical behaviour of a system in thermal equilibrium at fixed temperature, volume, and particle number. From , one can derive key thermodynamic functions such as pressure, internal energy and entropy through straightforward mathematical relations.
In the previous article, we derived the expressions for pressure and internal energy:
_{T,N}\;\;\;\;\;\;\;\;146)
_{V,N}\;\;\;\;\;\;\;\;148)
where 
and 
.
Question
How does _{T,N})
connect quantum mechanics to thermodynamics?
Answer
, the pressure of a system, is a macroscopic thermodynamic property, while 
is the energy of a quantum mechanical microstate, which is an eigenvalue of the Hamiltonian. Therefore, the equation provides a bridge between the microscopic quantum description and macroscopic thermodynamic observables.
The corresponding expression for entropy 
can be derived by first dividing the fundamental equation of thermodynamics by 
to give:
+\frac{U}{T^2}dT+\frac{P}{T}dV\;\;\;\;\;\;\;\;156)
Applying the chain rule to eq148 gives:
_{V,N}\biggr\(\frac{d T}{d \beta}\biggr\)=kT^2\biggr\(\frac{\partial lnQ}{\partial T}\biggr\)_{V,N}\;\;\;\;\;\;\;\;157)
Substituting eq146 and eq157 into eq156 yields:
+k\biggr\(\frac{\partial lnQ}{\partial T}\biggr\)_{V,N}dT+k\biggr\(\frac{\partial lnQ}{\partial V}\biggr\)_{T,N}dV\\&=d\biggr\(\frac{U}{T}\biggr\)+kdlnQ\;\;\;\;\;\;\;\;158\end{align})
Integrating eq158 results in 
, where 
is a constant. As 
, only the ground state 
is populated. Assuming the ground state is non-degenerate, the partition function becomes 
, with 
. According to the third law of thermodynamics, entropy approaches zero as the temperature approaches absolute zero. Therefore, must be zero to satisfy this requirement, resulting in:
_{V,N}+klnQ\;\;\;\;\;\;\;\;159)
It follows that the Helmholtz energy expression is:
Using the pressure and internal energy equations, the expression for enthalpy is:
_{V,N}+VkT\biggr\(\frac{\partial lnQ}{\partial V}\biggr\)_{T,N}\;\;\;\;\;\;\;\;159b)
Question
Does eq159b contradict the application of enthalpy, which describes a system at constant pressure?
Answer
The definition of enthalpy, 
, holds for any thermodynamic state, regardless of whether the pressure is constant. The condition of constant pressure becomes relevant when evaluating the change in enthalpy, 
, which equals the heat exchanged in a constant-pressure process 
. Eq159b expresses the enthalpy of a system in terms of 
, 
and . It gives the enthalpy for a particular equilibrium state, not just under constant pressure. Therefore, we can calculate the enthalpy of a system at any given state using eq159b. By evaluating it at two different states (e.g. the initial and final states of a process), we obtain . If the process connecting those states occur at constant pressure, then 
. So, there is no contradiction.
The expression for constant-volume heat capacity is:
_{V,N}\\&=k\biggr\[\frac{\partial T^2\biggr\(\frac{\partial lnQ}{\partial T}\biggr\)}{\partial T}\biggr\]_{V,N}\\&=KT^2\biggr\(\frac{\partial^2 lnQ}{\partial^2 T}\biggr\)_{V,N}+2kT\biggr\(\frac{\partial lnQ}{\partial T}\biggr\)_{V,N}\;\;\;\;\;\;\;\;159c\end{align})
For Gibbs energy, we have 
. Hence,
_{T,N}\;\;\;\;\;\;\;\;159d)
If we define chemical potential as _{T,V})
, and is an integer-valued discrete variable, then the derivative becomes a finite difference, so:
\;\;\;\;\;\;\;\;159e)