Thermodynamic functions involving the molecular partition function describe the macroscopic thermodynamic properties of solids and ideal gases composed of non-interacting particles in the canonical ensemble.
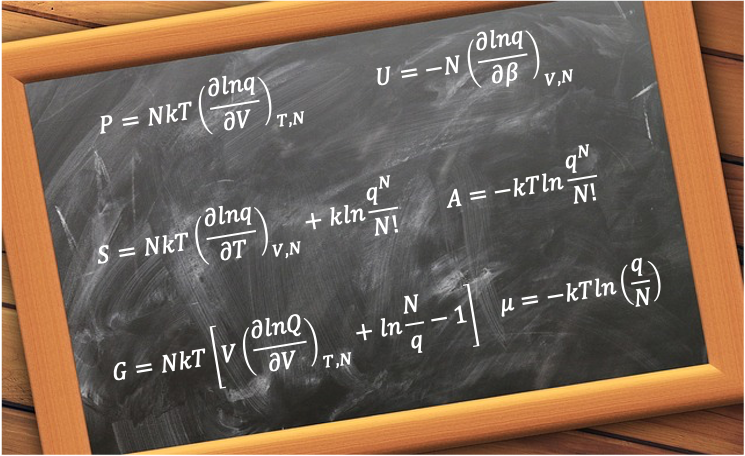
These functions are derived using thermodynamic functions involving the canonical partition function :
| Thermodynamic Property | Function | Derivation |
| Pressure | eq146 | |
| Internal energy | ||
| Entropy | eq159 | |
| Helmholtz energy | eq159a | |
| Enthalpy | eq159b | |
| Constant-volume heat capacity | eq159c | |
| Gibbs energy | eq159d | |
| Chemical potential | eq159e |
For example, substituting eq166 into eq157 yields the internal energy for a system of non-interacting, distinguishable particles (such as those in a solid):
Here, is the total single-particle partition function (i.e. eq257), with contributions from translational, rotational, vibrational and electronic degrees of freedom. Eq320 assumes that all components of
, including
, are defined using absolute energy levels — for example, the vibrational molecular partition function includes the zero-point energy (i.e. eq290). However, if
is instead defined relative to the zero-point energy (i.e. eq292), then we need to add back the zero-point energy term
giving:

Question
Show how eq320 is applicable to a system in which particles can occupy two states with absolute energies 0 and .
Answer
From eq250, . Therefore,
As ,
, which implies that all particles are in the ground state. As
,
. This is also physically intuitive. At very high temperatures, thermal energy far exceeds the energy gap
. The two energy states are equally populated, and the average energy per particle is
. The total internal energy is therefore
times this average energy.
The above Q&A demonstrates that although the molecular partition function is defined for a single particle, thermodynamic functions derived from it describe the macroscopic properties of a system. In the case of an ideal gas (composed of non-interacting, indistinguishable particles), substituting eq167 into eq157 also results in eq320. Similarly, for non-interacting, indistinguishable particles, each of the expressions for pressure , enthalpy
and constant-volume heat capacity
in terms of the molecular partition function is the same. They are given by:

Question
Compare the expressions for pressure derived from the canonical partition function and the molecular partition function.
Answer
Comparing eq322 and eq146,
|
Aspect |
||
|
Dependence |
Canonical (full system) partition function |
Molecular (single-particle) partition function |
|
Assumed interactions |
Valid for both interacting and non-interacting particles |
Assumes non-interacting, indistinguishable particles |
| Application | Real gases |
Ideal gases |
However, the statistical thermodynamic expressions for entropy , as well as for Helmholtz energy, Gibbs energy and chemical potential, differ between distinguishable and indistinguishable particles due to the Gibbs paradox. For an ideal gas, substituting eq167 into eq159 results in:
It follows that the Helmholtz energy expression for an ideal gas is:
For Gibbs energy, we have . Hence,

Question
Show that .
Answer
Substituting into eq326 yields
, where
. For an ideal gas,
, where
is the number of moles and
, with
being the Avogadro constant. So,
where .
Using Stirling’s approximation and ,
where is the molar molecular partition function.
Dividing eq328 through by gives:
Substituting eq167 into eq159e gives the expression for the chemical potential of an ideal gas: