Time dilation is the difference in time measured by an observer who is moving relative to another observer.
Consider two frames of reference, each with an observer and a clock, which consists of a photon bouncing between two mirrors A and B. If the frame of observer X is at rest, while the frame of observer Y is moving away from it, observer Y sees the photon of his clock travelling vertically between the mirrors (diagram I) and measures , where
is known as the proper time,
is the distance between the mirrors and
is the speed of light.
Observer X, however, sees the same photon moving in a triangular path (as observer Y’s clock moves away from him) and measures (diagram II), where
is the time recorded using his own clock.
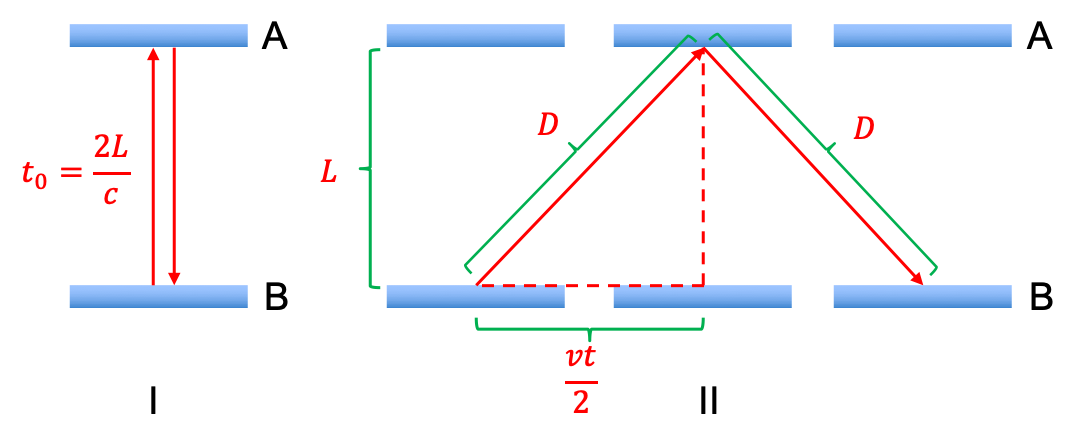
Substituting , where
is the speed of the moving frame relative to the rest frame, and
in
, we have
where is called the Lorentz factor, which is useful in deriving the Thomas half.
Eq249 states that the time interval measured by an observer who is stationary relative to the moving clock for events occurring on the moving clock will always be longer than the time interval measured by someone at rest with respect to the clock. This longer time interval means that, from the perspective of the stationary observer, the moving clock is slowing down relative to the observer’s own clock. In other words, the stationary observer will see the moving clock as ticking more slowly, and the time measured by the moving clock will seem dilated or stretched from the viewpoint of the stationary observer.