The translational molecular partition function is a measure of the number of thermally accessible translational energy states available to a single non-interacting molecule in a given volume at a specific temperature.
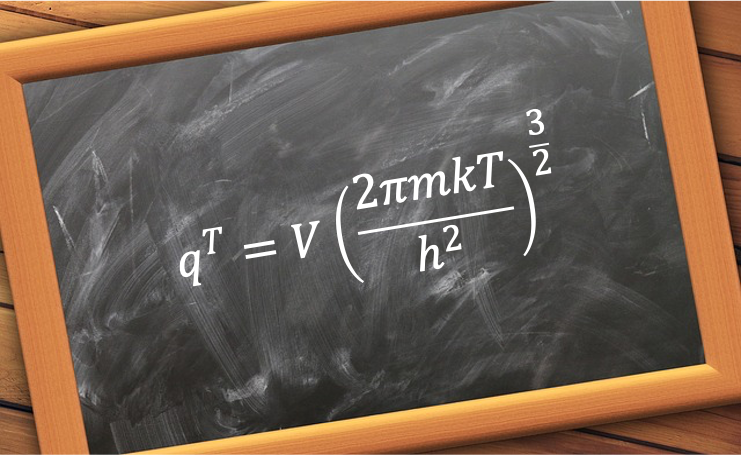
Consider a particle of mass moving freely in a three-dimensional box of lengths
,
and
. Its translational energy
is given by eq45h:
where ,
,
, with
.
Substituting eq260 into the translational component of eq257 gives:
where ,
and
.
To simplify eq261, we need to evaluate the three summations, each of which can be approximated as an integral. For example:
This approximation is valid because the exponential term varies smoothly with for a particle in a laboratory-scale vessel, where
is typically on the order of 10-20 or smaller. It follows that
for
. Therefore,
. On the other hand, the full integral
is a well-known Gaussian integral:
If is a very small number, then eq263 evaluates to a very large value (typically on the order of 1010). Therefore, we can change the lower limit of the integral in eq262 from 1 to 0 with negligible error:
From the identity (see this article for derivation), we have
since the integrand is an even function (symmetric about the vertical axis). Therefore, eq264 evaluates to:
Similarly, we have and
, with eq261 becoming:
where is the volume of the vessel.
By considering the energy levels that result from motion in three-dimensional space, the translational partition function enables the calculation of macroscopic properties such as pressure, entropy and internal energy for ideal gases. This function is especially crucial for connecting microscopic molecular behaviour with observable bulk thermodynamic quantities.