Vibration-rotation spectra of polyatomic molecules

Vibration-rotation spectra arise from the simultaneous vibrational and rotational transitions of molecules, typically observed in the infrared (IR) region of the electromagnetic spectrum. These spectra provide detailed information about molecular structure, bond strength, and moment of inertia.

For a molecule to be IR active, it must have a permanent dipole or a dipole moment that changes over time. Since polyatomic molecules have vibrational modes, some which do not result in a change in the molecules’ dipole moments, only certain vibration-rotation transitions are IR active. The transition selection rules are given by eq7 or eq8b, depending on whether the molecule is linear or non-linear.

 

Linear molecules

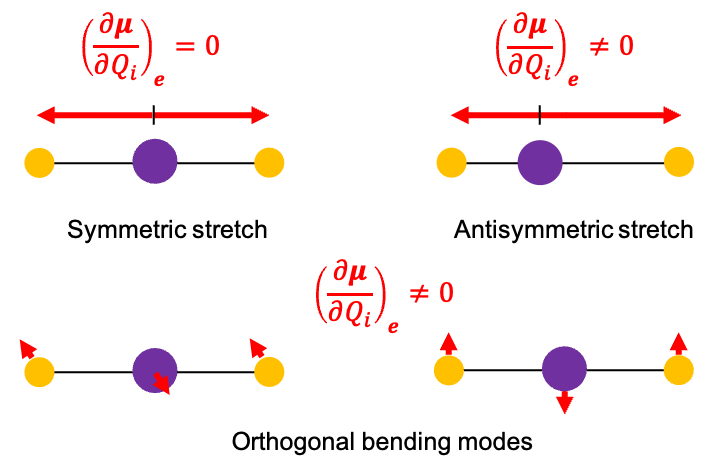
An example of a polyatomic linear molecule is CO₂, which has the same expressions for , and as those for diatomic molecules. The symmetric stretch of CO₂ is IR inactive because the net electric dipole moment is always zero (see diagram above).

 

 

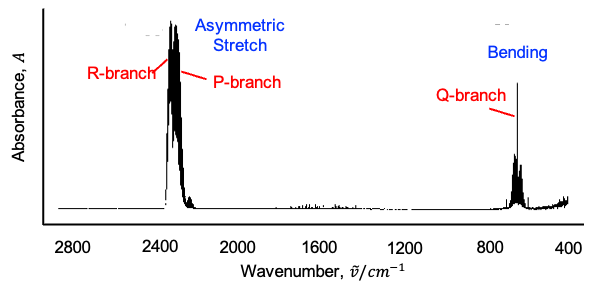
In contrast, the antisymmetric stretch is IR active because it produces a dipole moment that varies with displacement. Since CO₂ is a closed-shell molecule, . Furthermore, this vibrational mode does not produce vibrational angular momentum (). Therefore, the absorption of the photon’s angular momentum must be accounted for by , resulting in (P-branch or R-branch).

The degenerate bending modes are also IR active but differ from the asymmetric stretch in an important way: they can involve vibrational angular momentum. Because the two bending modes occur in perpendicular planes and are degenerate, their linear combination can produce a circular (or elliptical) motion of the O atoms about the C atom, effectively giving rise to vibrational angular momentum. This allows the molecule to absorb the photon’s angular momentum along an alternate pathway without requiring a change in the rotational quantum number. In other words, after photon absorption, but the vector addition of and can result in the magnitude of being unchanged (possible when ), enabling transitions to appear in the IR spectrum as the Q-branch.

 

Symmetric tops

For a symmetric top, its molecular rotational energy is given by eq51. Therefore, eq9 becomes:

Any allowed vibrational transition of a symmetric rotor like CH₃I can involve a change in the dipole moment along the molecule’s symmetry axis (known as a parallel transition), as well as changes in and , which are perpendicular to (perpendicular transitions). The general selection rules governing parallel transitions for symmetric rotors are given by eq8:

while those for perpendicular transitions are given by eq8a:

It follows that the parallel transition expressions for , and  are the same as those for linear molecules. For perpendicular transitions, each branch has two sub-branches depending on :

 

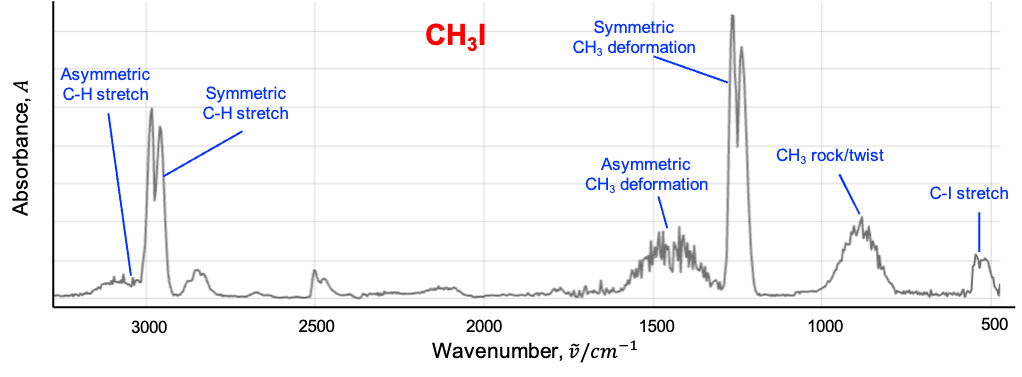
Therefore, the IR spectrum for CH₃I (see diagram above) is more complicated than that for CO₂. Furthermore, there are vibrational modes, which are categorised into six types:

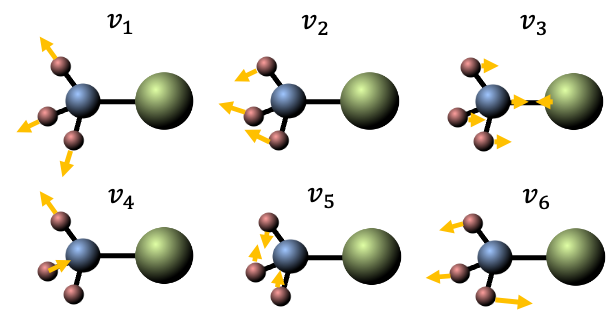
The first three modes are symmetric vibrations (see diagram below), with a change in dipole moment parallel to the C₃ axis. The remaining three modes are doubly degenerate asymmetric vibrations, with a change in dipole moment perpendicular to the C₃ axis.

 

Spherical tops

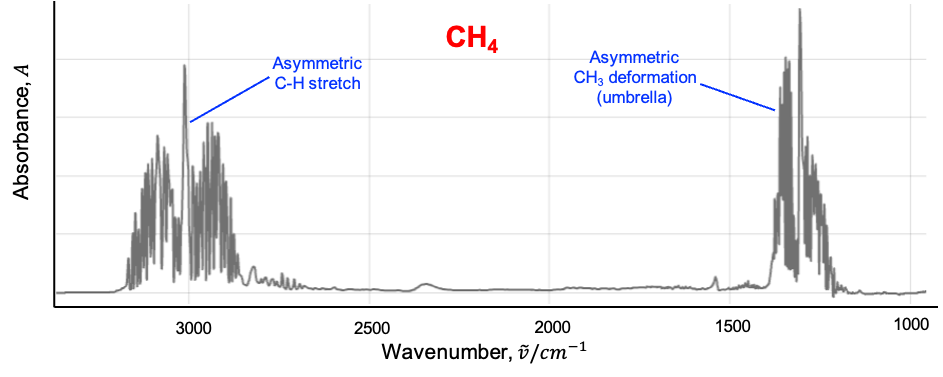
Although a spherical top is non-polar overall, some of its vibrational modes are IR active due to temporary dipole moments during vibration. The first-order approximation of the vibration-rotation energy levels of a spherical top is also given by eq9, with the selection rules governing IR-active transitions between these levels being the same as those for linear molecules. An example is CH₄, which has vibrational modes (see table and diagram below): one symmetric stretch, one doubly degenerate bend, and two triply degenerate modes (one stretch and one bend).

Mode	Symmetry	Description	Wavenumber /cm-1
		Symmetric C-H stretch	IR inactive
		Symmetric bend (scissoring)	IR inactive
		Asymmetric C-H stretch	3020
		Asymmetric bend (umbrella)	1300

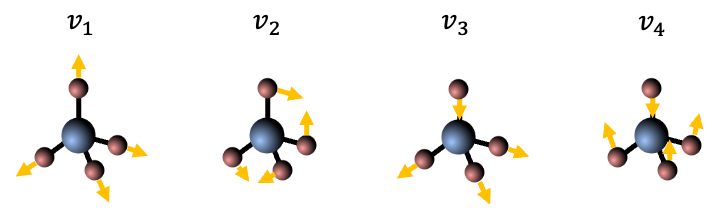
However, only the modes are IR active due to their symmetry and ability to cause a dynamic dipole moment (see diagram below).

In conclusion, the derivation of the three branches using the first-order vibration-rotation energy levels (eq9 and eq17) of an IR-active polyatomic molecule allows us to analyse most IR spectra with ease. However, these energy levels are more complex due to changes in at higher , centrifugal distortion, anharmonicity and vibration-rotation interactions such as Coriolis coupling.

 

Next article: coriolis effect and Coriolis coupling

Previous article: Vibration-rotation spectra of diatomic molecules

Content page of rovibrational spectroscopy

Content page of advanced chemistry

Main content page