The weak-field limit of the Zeeman effect is the regime in which an atom or molecule in an external static magnetic field exhibits splitting of its spectral lines into multiple components, with the field strength small compared to the internal spin–orbit interaction.
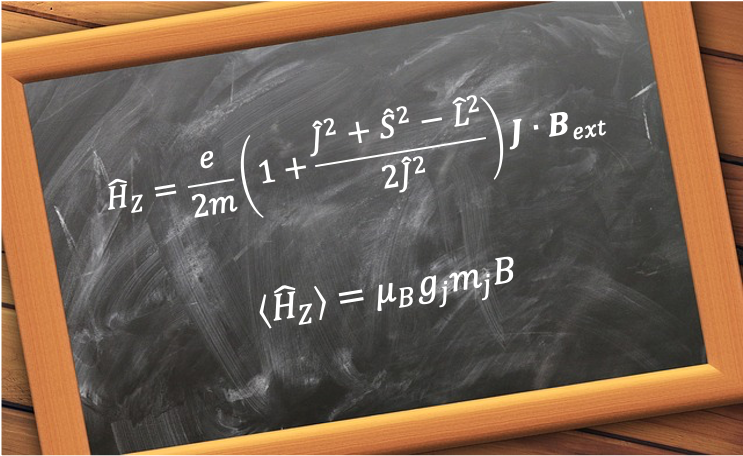
To analyse the weak-field regime, we consider a hydrogen atom in the field . As mentioned in this article,
is a good quantum state to describe the system in the absence of an external magnetic field, with both
and
precessing rapidly about their vector sum
. So, if the external magnetic field is weak, where
, we can assume that
remains good, with the time-average of
being its projection along
:
where is a unit vector, not an operator.

Question
Why is a good quantum number when
precesses around
?
Answer
During precession, the direction of changes but its magnitude
is conserved. Since the quantum number
is associated with the eigenvalues of the operator
, and since
(see this article and this article for explanation),
is a good quantum number. On the other hand,
,
, so
and
are not good quantum numbers in the absence of an external magnetic field.
Since ,
Because ,
Substituting eq332 back into eq331 gives:
If we take the -axis along the direction of the external field, where
(
being a unit vector),
Taking the expectation value of yields:

Question
Prove that if , then
.
Answer
From , we have
. Since
, it follows that
or equivalently,
.
Substituting the eigenvalues of the corresponding operators into eq333 results in
which may be written as
where is the Bohr magneton and
is the Landé facrtor.
Comparing eq330 and eq334, the Zeeman interaction introduces an energy shift proportional to , thereby lifting the degeneracy of the energy levels that exists in the absence of an external magnetic field. This lifting of degeneracy is the essence of the Zeeman effect. For example, substituting the quantum numbers
into eq334, the ground state of the hydrogen atom splits into two levels with energies
.

Question
Describe the weak-field Zeeman effect on the hydrogen atom configuration of 2p1, with and
.
Answer
In the absence of an external magnetic field, spin-orbit coupling (using LS coupling) splits the 2p1 configuration into two energy levels, and
, with degeneracies
and
respectively. A weak external magnetic field lifts the remaining magnetic degeneracy, as indicated in the table below.