There are 3 types of cubic unit cells: primitive, body-centred and face-centred.
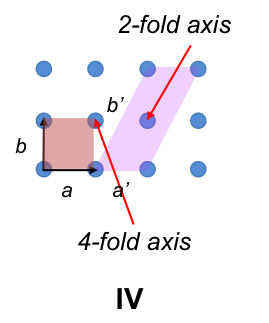
A three-dimensional Bravais lattice with 4-fold rotational symmetry is created by stacking figure IV lattices one above another (IVa), resulting in the primitive cubic unit cell (IVb) with IaI = IbI = IcI and α = β = γ = 90o.
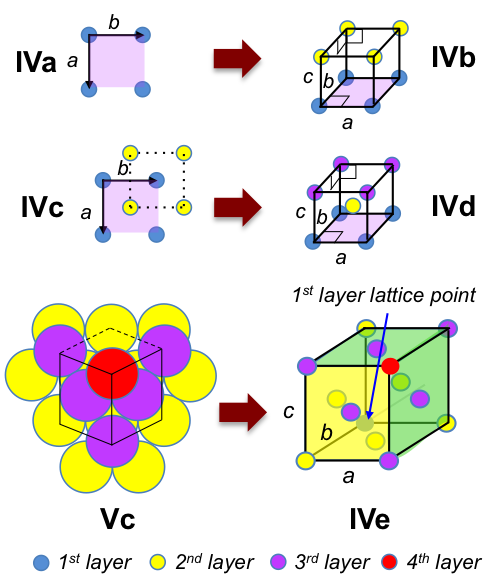
If we stagger the second layer so that the lattice points are in the middle of squares formed by the first layer (IVc), followed by a third layer that is directly above the first layer, we have the non-primitive body-centred cubic unit cell (IVd) with IaI = IbI = IcI and α = β = γ = 90o.
The primitive cubic unit cell can also be formed via the triple hexagonal lattices of Vc when the perpendicular distance between two layer of lattices is (IaI√6)/6 (see next article for proof). Similarly, the face-centred cubic unit cell (IVe) with IaI = IbI = IcI and α = β = γ = 90o, is created via the triple hexagonal lattices of Vc when the perpendicular distance between two layer of lattices is (IaI√6)/3 (see next article for proof).
Even though it is possible to define three-dimensional primitive rhombohedral unit cells for the body-centred cubic and face-centred cubic lattices, these primitive cells are typically not used to represent the two lattices, as they do not reveal the higher rotational symmetry of the cubic lattices and are difficult to visualise due to their inter-axial angles not being 900.
