Space lattices that are composed of orthorhombic unit cells are formed by stacking two-dimensional lattices depicted in figure II (where IaI ≠ IbI and the angle between the basis vectors is not 90o) in three different ways such that the space lattice maintains a 2-fold rotational symmetry.
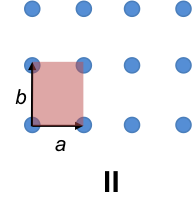
The first way is to stack successive layers that are directly above one another (IIa), resulting in the primitive orthorhombic unit cell (IIb), with IaI ≠ IbI ≠ IcI and α = β = γ = 90o.
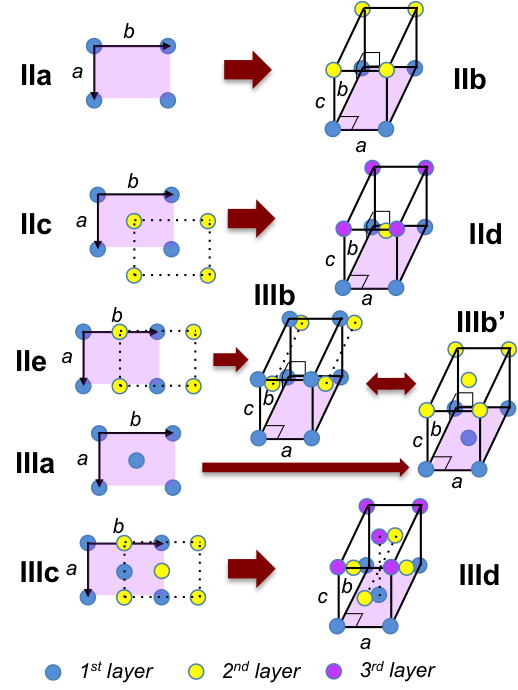
The second way is to stack a second layer such that its lattice points are in the middle of rectangles formed by the lattice points of the first layer (IIc). A third layer is then stacked directly above the first layer, giving a non-primitive unit cell known as body-centred orthorhombic (IId) with IaI ≠ IbI ≠ IcI and α = β = γ = 90o.
The third way is to stack a second layer such that its lattice points are in between the lattice points of the first layer (IIe). A third layer is then stacked directly above the first layer, resulting in a non-primitive unit cell called base-centred orthorhombic (IIIb), with IaI ≠ IbI ≠ IcI and α = β = γ = 90o.
The base-centred orthorhombic unit cell (IIIb) happens to be the same unit cell obtained by stacking the two-dimensional lattices of figure III (see diagram below) directly above one another (IIIa) to give figure IIIb’ (see above diagram).

We have used the non-primitive unit cell (IIIa) of the two-dimensional lattice of figure III as the reference cell to form IIIb’ instead of the primitive rhombic unit cell. This is because the resultant three-dimensional unit cell that is formed by IIIa is easier to visualize and reveals the higher symmetry of the orthorhombic C lattice than the resultant unit cell formed by the primitive rhombic unit cell.
The other way to generate a lattice (using figure III) with a 2-fold rotational symmetry is to stagger the second layer as shown in IIIc, with a third layer directly above the first layer. This gives a non-primitive unit cell called face-centred orthorhombic (IIId), with IaI ≠ IbI ≠ IcI and α = β = γ = 90o. All orthorhombic unit cells are described by the same parameters of IaI ≠ IbI ≠ IcI and α = β = γ = 90o. All orthorhombic unit cells also have three perpendicular two-fold rotational axes.
