Tetragonal unit cells are found in space lattices that are formed by stacking the same two-dimensional lattices as those for space lattices containing orthorhombic unit cells, i.e. either figure II or figure III.

For space lattices containing orthorhombic unit cells, the layers of either figure II or figure III are stacked such that IaI ≠ IcI. If the layers are stacked at a height such that IaI = IcI, we get two new unit cells: primitive tetragonal (IIf) and body-centred tetragonal (IIg), both of which have the parameters IaI ≠ IbI = IcI and α = β = γ = 90o.

The unit cell IIh that is derived from the stacking of either IIe or IIIa (with IaI = IcI), is equivalent to the primitive tetragonal unit cell IIf. Similarly, the unit cell IIIi that is derived from the stacking of IIIc (with IaI = IcI) is equivalent to the body-centred tetragonal unit cell IIg.
We can rename the basis vectors so that the parameters for a primitive tetragonal unit cell and and those for a body-centred tetragonal unit cell are IaI = IbI ≠ IcI and α = β = γ = 90o, which are the conventional parameters of a tetragonal unit cell. Both tetragonal unit cells can also be formed by stacking layers of the two-dimensional lattice of figure IV (see diagram below).
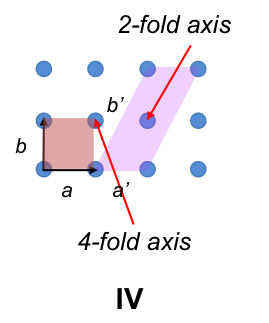
Finally, a tetragonal unit cell has one 4-fold rotational axis of symmetry since it has two opposite faces that are squares.
