Bragg’s law states that the incidence and scattered waves in x-ray diffraction make the same angle with a lattice plane.
X-ray is a form of electromagnetic radiation, which has an alternating electric field component. When a beam of X-rays encounters a charged particle, such as an electron in an atom, its rapidly alternating electric field causes the electron to oscillate and form a dipole. Since an accelerated charge emits electromagnetic radiation, the accelerated electron (sinusoidal change of velocity with time) reemits X-ray at the same frequency as the incident radiation. This phenomenon is known as scattering.

X-ray diffraction is a technique that relies on the interference of X-rays, which are scattered by atoms in a crystal, for analysing properties of the crystal. As the overall electron density of an atom is approximately spherical, X-ray scattered by the atom is consequently spherical (see diagram below). This is analogous to the atoms being the source of spherical wavelets, as stated in Huygens’ principle. The scattered X-rays therefore interfere with one another to form a distinct pattern.
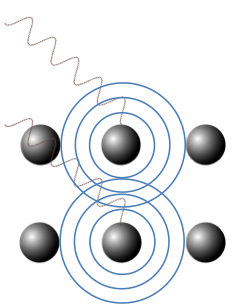
In 1913, William Bragg and his son Lawrence Bragg considered the specular waves scattered by atoms in a crystal, i.e., incident and scattered waves that make the same angle with a lattice plane (see diagram below). They proposed that scattered specular X-ray waves, from atoms separated by an interplanar distance dhkl, interfere constructively when the difference between their respective total path lengths, which is AB + BC, is an integer multiple of the wavelength of the X-ray.
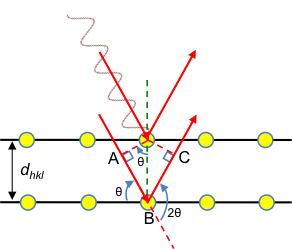
So, according to Bragg’s law:
where n ∈ and n is called the order of diffraction.
Since both the order of diffraction and the common factor between planes are integers, we can substitute eq5 where dhkl = ndnh,nk,nl in eq10:
Combining eq7 where for a primitive cubic unit cell and eq11, we have:
where n is now the common factor between planes.
This eliminates the need to describe a signal in terms of the order of diffraction. In other words, each signal now refers to the first order diffraction from the (nh nk nl) plane. Eq12 is often written simply as:
because it is understood that h = nh, k = nk and l = nl.
The significance of eq12 and eq13 is that a set of lattice planes, with a specific Miller index (hkl) in a solid composed of a particular unit cell dimension, scatters X-rays that interfere constructively at a specific specular angle. Therefore, eq12 and similar equations for other unit cell types allow us to determine unit cell dimensions, if the angle of diffraction and the Miller index (hkl) are known. This is accomplished experimentally via X-ray diffraction techniques, one of which is powder X-ray diffraction.

Question
What if we consider a scattered X-ray vector in a different direction with respect to the one used in Bragg’s law, e.g. one that points below the lattice plane?
Answer
You get a different constructive interference (diffraction) formula known as the Laue equations, i.e., you have a different mathematical approach using different criteria to describe the same diffraction pattern.
