A unit cell is a parallelepiped that is the simplest repeating unit of a crystal. A unit cell must fill all space of the crystal when replicated. As a result, spherical unit cells do not exist.
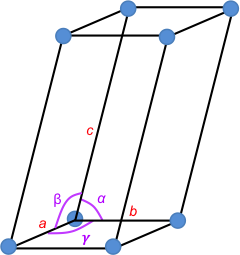
At each corner of the unit cell is a blue point known as a lattice point (see above diagram). The environment of any lattice point is equivalent to the environment of any other lattice point in the crystal. An infinite three-dimensional array of lattice points forms a three-dimension lattice called a space lattice. A unit cell that only has lattice points at its corners is called a primitive unit cell. Unit cells are sometimes chosen in the non-primitive form for convenience.
The edges of a unit cell are, by convention, chosen to be right-handed (a × b is the direction of c). The angles α, β and γ are between b and c, c and a, and a and b respectively.
