What is the formula of the titration curve of a monoprotic strong acid versus a monoprotic weak base?
We make use of eq1 from a previous article except that Cb is now the concentration of a weak base. Since the weak base is partially ionised in water, at any point of the titration, the sum of the number of moles of BOH and B+ must equal to the number of moles of BOH if it were undissociated. As the change in volume of the solution is common to all ions,
where Va and Vb are the volume of strong acid in the solution and the volume of weak base in the solution respectively. Substitute in eq9 where Kb is the dissociation constant of BOH and rearranging, we have,
Substitute eq10, eq2, Kw = [H+][OH–] and [H+] = 10-pH in eq1,
Eq11 is the complete pH titration curve for a monoprotic strong acid versus monoprotic weak base system. We can input it in a mathematical software to generate a curve of pH against Va. For example, if we titrate 10 cm3 of 0.200 M of aqueous NH3 (Kb = 1.8 x 10-5) with 0.100 M of HCl, we have the following:
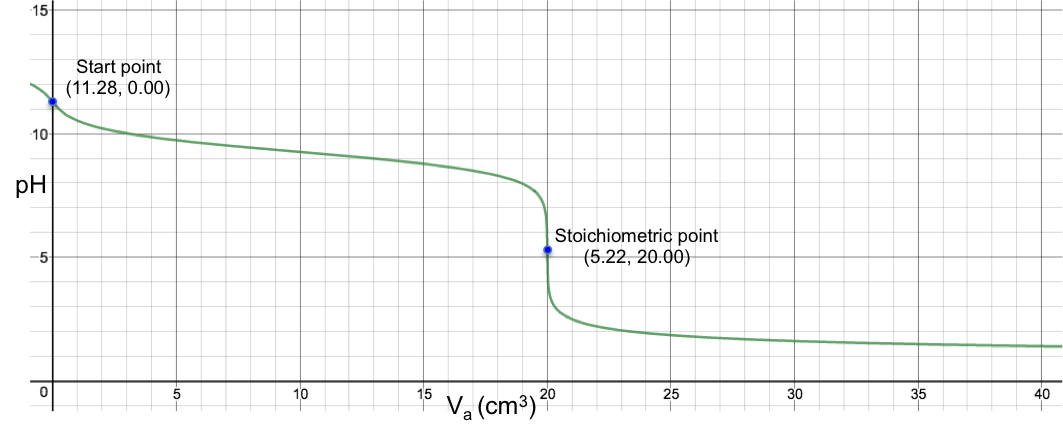
To understand the change in pH near the stoichiometric point versus the change in Va, we assume that one drop of acid is about 0.05 cm3 and substitute 19.95 cm3, 20.00 cm3 and 20.05 cm3 into eq11. The respective pH just before and just after the stoichiometric point (SP) are:
|
|
One drop before SP | SP |
One drop after SP |
|
Volume, cm3 |
19.95 | 20.00 |
20.05 |
|
pH |
6.65 | 5.22 |
3.78 |
The data shows that two drops of acid cause a change of 2.87 in pH before and after the stoichiometric point. Since the change in pH at the stoichiometric point is smaller than that of a strong acid versus strong base titration, we can use fewer indicators that work within the range to monitor the titration. Lastly, we can derive the gradient equation for a strong acid to weak base titration and investigate the inflexion point at pH 5.22 by differentiating eq11 implicitly (see previous article), resulting in , i.e. a gradient that makes angle of –89.52o with the horizontal.