We have mentioned in a quantum chemistry article that the nucleus of an atom (e.g. 1H and 13C) possesses an intrinsic angular momentum called spin I and therefore a magnetic dipole moment μ, which tends to align parallel to an external magnetic field B in two possible directions (see diagram below).
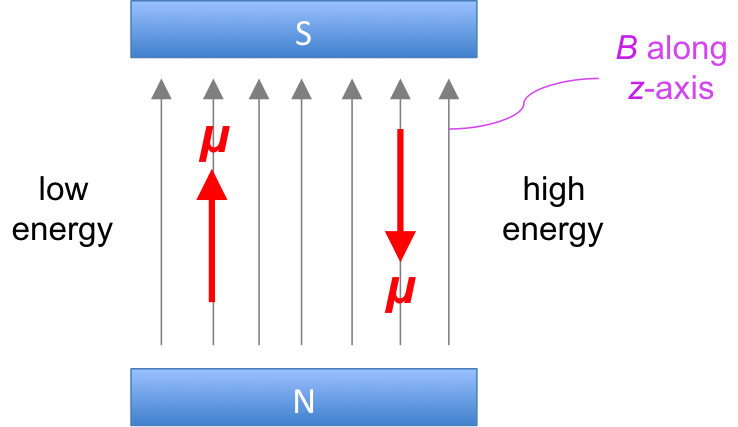
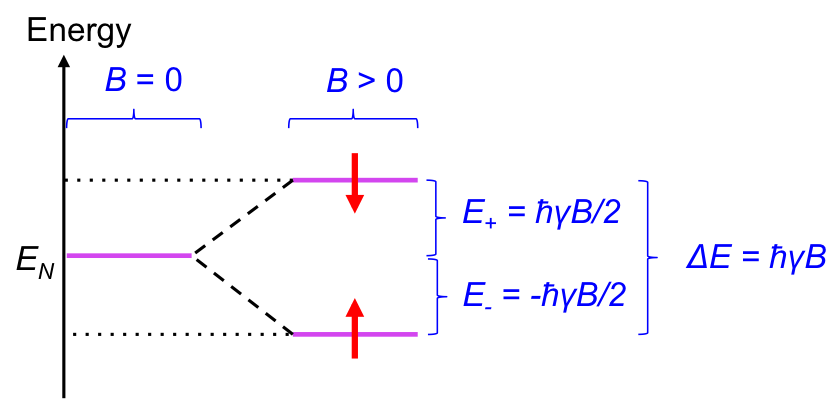
Like tiny magnets, we would expect all dipoles of a sample of nuclei to align in the direction of an external field to achieve a lower energy state. However, at room temperature, the dipoles are constantly exchanging between the two forms, to the extent that at equilibrium, there is a slight excess of nuclei with dipoles that are aligned in the direction of the field. This behaviour of nuclear magnetic dipole moments in the presence of an external magnetic field at room temperature splits the energy of nuclei EN into two levels (see diagram below).
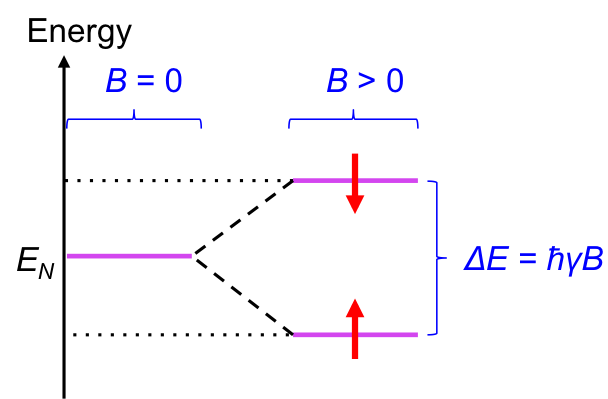
It is found that the energy gap between the two levels ΔE is proportional to the external magnetic field:
where is proportionality constant, with
being the gyromagnetic ratio, whose value is dependent on the identity of the nucleus.
Due to the slight excess of nuclei at the lower level at room temperature when B > 0, a net upward spin transition occurs when the nuclei are excited with radiation corresponding to ΔE. As the gyromagnetic ratio is nuclide-specific, ΔE varies for different nuclide at a fixed value of B. Furthermore, the effective external magnetic field Beff experienced by a nucleus is dependent on the magnetic environment of the nucleus, which changes eq1 to:
Eq2 is the heart of the analytical technique of nuclear magnetic resonance, where the identity and location of an unknown nuclide is determined by exposing the nuclide to a constant magnetic field and subsequently detecting its transition frequency.

Question
What are the typical frequencies for nuclear spin transitions? Why are nuclei with I = 0 not NMR active?
Answer
The frequencies needed for nuclear spin transitions, called resonance frequencies, are in the radiofrequency range. For example, γ for 1H that is exposed to an external magnetic field of 9.4 T is 26.75 x 107 T-1s-1. Substituting these values and the Planck relation ΔE = hv in eq1, we have v = 400.2 MHz.
A nuclide with spin I = 0 is associated with the nuclear magnetic spin number of mI = 0, resulting in = 0. However, a nuclide with spin I = ½ has the nuclear magnetic spin numbers of mI = +½ and mI = -½, which gives: