In classical electrodynamics, a magnetic dipole moment is associated with a current loop (see diagram below), and represents the magnitude and orientation of a magnetic dipole. It is a pseudo-vector, whose direction is perpendicular to the plane of the loop and given by the right hand thumb rule.
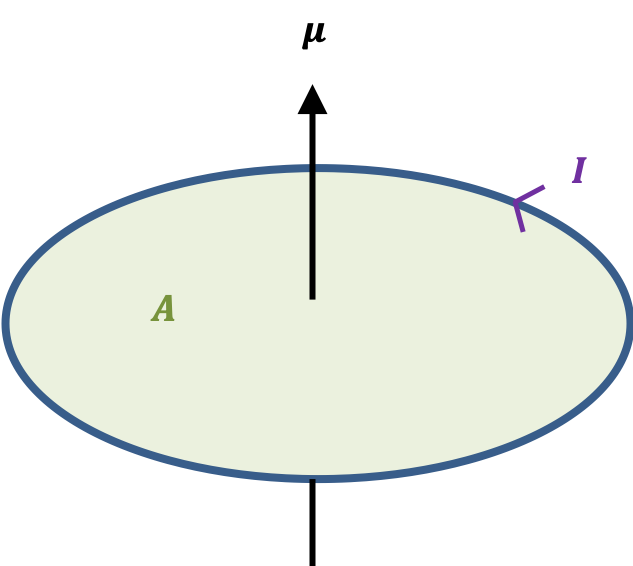
The magnitude of a magnetic dipole moment of a current loop is defined as
where is current, and
is the area of the loop.
Rewriting eq60 in terms of (where
is charge,
is time and
is the tangential velocity of the charged particle) and using
, we have
, where
is the mass of the charged particle. Substitute eq59 in
, we have the relation between magnetic dipole moment and angular momentum:
where is the classical gyromagnetic ratio.
When placed in an external magnetic field , the magnetic dipole moment experiences a torque, whose energy is

Question
How is eq62 derived?
Answer
In order to rotate a current loop, we must do work against the torque
due to the magnetic field
. For a rotating system (see diagram I below),
, where according to convention, the negative sign is added so that work on the system by the field is positive.
For small ,
. Since
and
, we have
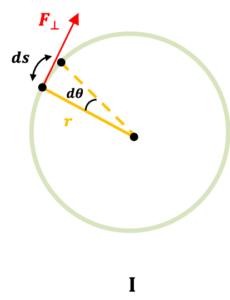
Diagram II below shows a square current loop with side 1 parallel to side 3 and side 2 parallel to side 4 (not shown in diagram). The length of each side is .
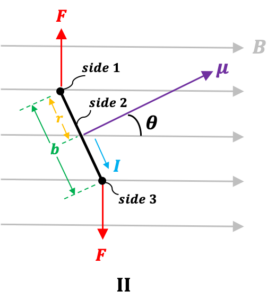
Since and
(
),
where is the area of the loop.
Substitute eq60 in the above equation,
Comparing eq62a and eq62b, torque can also be expressed as
The torque exerted by the magnetic field on the magnetic dipole tends to rotate the dipole towards a lower energy state. So, we let with
and eq63 becomes
, or simply:
Other than a torque, the external magnetic field may exert another force on the current loop. For a magnetic field pointing in the -direction,
, where
is a scalar function. We substitute eq65 in
to give
where ,
and
are unit vectors, and
is the gradient of the external magnetic field along the
-direction.
For a uniform field, (i.e. a constant) and
; while for an inhomogenous field,
, where
is a scalar representing the change in
along the
-axis, and
.
Substituting eq61 in eq62,
For an inhomogenous magnetic field pointing in the -direction, the above equation becomes
Eq68 is used as a starting point in analysing results from the Stern-Gerlach experiment.

Question
Does the magnetic field violate Maxwell’s 2nd equation of
where
?
Answer
The field should be , which satisfies
. However, the precession of the spin magnetic moment of a silver atom around
in the Stern-Gerlach experiment is so fast that the
-component of the spin moment averages to zero, resulting in an effective field of
interacting with the atom.

Question
Why is ?
Answer
A simple way of showing is to consider a two-dimensional diagrammatic representation of the vector function
below, where each point in the two-dimensional space is associated with a vector.
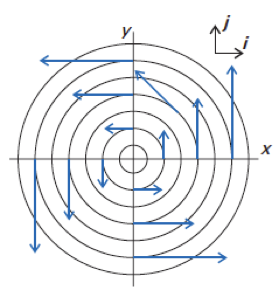
When , the successive points in the negative
direction and the positive
direction are associated with the vectors
and
respectively. Similarly, when
, the successive points in the negative
direction and the positive
direction are associated with the vectors
and
respectively. Clearly,
.
