Larmor precession of an electron

Larmor precession is the change in orientation of the axis of the magnetic moment of a particle with respect to the axis of an external magnetic field.

Consider an electron at rest with intrinsic spin angular momentum of $\boldsymbol{s}$ in a uniform magnetic field $\small \boldsymbol{\mathit{B}}$ directed along the $z$ -axis. The electron’s spin gives rise to a magnetic dipole moment $\small \boldsymbol{\mathit{\mu}}$ , which is antiparallel to $\boldsymbol{s}$ . As a result, the magnetic field interacts with the electron’s magnetic moment and generates a torque $\small \boldsymbol{\mathit{\tau}}=\boldsymbol{\mathit{\mu}}\times\boldsymbol{\mathit{B}}$ (see diagram below).

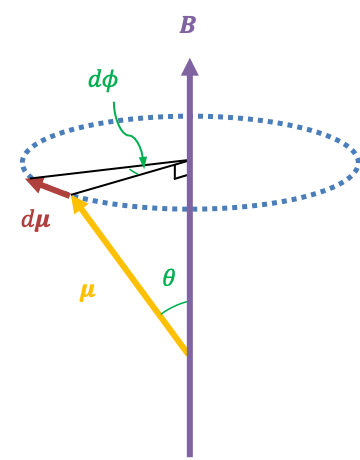
Eq61 becomes $\small \boldsymbol{\mathit{\mu}}=\gamma_e\boldsymbol{\mathit{s}}$ , where $\small \gamma_e$ is the gyromagnetic ratio of the electron. Taking the derivative on both sides of this equation with respect to $\small t$ ,

$\small \frac{d\boldsymbol{\mathit{\mu}}}{dt}=\gamma_e\frac{d\boldsymbol{\mathit{s}}}{dt}$

From eq64 and eq71, we have $\small \frac{d\boldsymbol{\mathit{L}}}{dt}=\boldsymbol{\mathit{\mu}}\times \boldsymbol{\mathit{B}}$ , whose spin analogue is $\small \frac{d\boldsymbol{\mathit{s}}}{dt}=\boldsymbol{\mathit{\mu}}\times \boldsymbol{\mathit{B}}$ . So,

$\small \frac{d\boldsymbol{\mathit{\mu}}}{dt}=\gamma_e\, \boldsymbol{\mathit{\mu}}\times \boldsymbol{\mathit{B}}$

Question

Explain in detail why $\boldsymbol{\mathit{\mu}}$ precesses around $\boldsymbol{\mathit{B}}$ .

Answer

Since $\frac{d\boldsymbol{\mathit{s}}}{dt}=\boldsymbol{\mathit{\mu}}\times \boldsymbol{\mathit{B}}$ , the torque arises from the interaction between the magnetic dipole moment and the external magnetic field causes the spin angular momentum to change in time. Because this torque is perpendicular to the magnetic field direction (taken as the $z$ -axis), it has no component along that axis. Consequently, the projection $s_z$ of the spin angular momentum onto the field direction remains constant. The only way for $\boldsymbol{s}$ to change in time while maintaining a constant projection along the $z$ -axis is for it to precess about the direction of the magnetic field.

With reference to the above diagram, the change in arc length with respect to $\small t$ is $\small \frac{d\mu}{dt}=\mu sin\theta\frac{d\phi}{dt}$ . Hence,

$\small \gamma_e\mu Bsin\theta=\mu sin\theta\frac{d\phi}{dt}$

$\small \int_{0}^{2\pi}d\phi=\gamma_eB\int_{0}^{T}dt$

$\small \omega_L=\vert\gamma_e B\vert=\frac{eB}{m_e}\; \; \; \; \; \; \; \; 149$

where $\small T$ is the period, $\small m_e$ is the mass of an electron and $\small \omega_L=\frac{2\pi}{T}$ is the Larmor frequency, which is defined as a positive value.