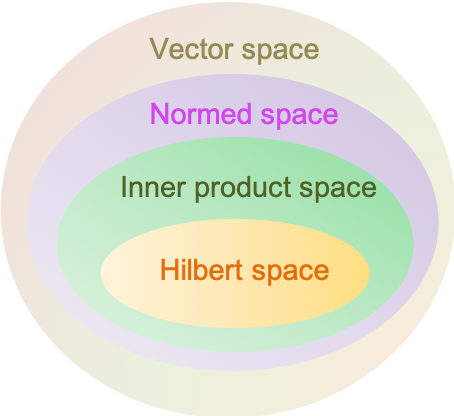
A Hilbert space is a complete inner product space. It allows the application of linear algebra and calculus techniques in a space that may have an infinite dimension.
The inner product in a Hilbert space has the following properties:
- Conjugate symmetry:
- Linearity with respect to the 2nd argument:
- Antilinearity with respect to the first argument:
- Positive semi-definiteness:
, with
if
The last property can be illustrated using the space that is equipped with an inner product. Such a space is an example of a real finite-dimensional Hilbert space. The inner product of the vector
with itself is:
We define a complete Hilbert space as one where every Cauchy sequence in converges to an element of
. If you recall, a Cauchy sequence is a sequence, e.g.
where
, for which
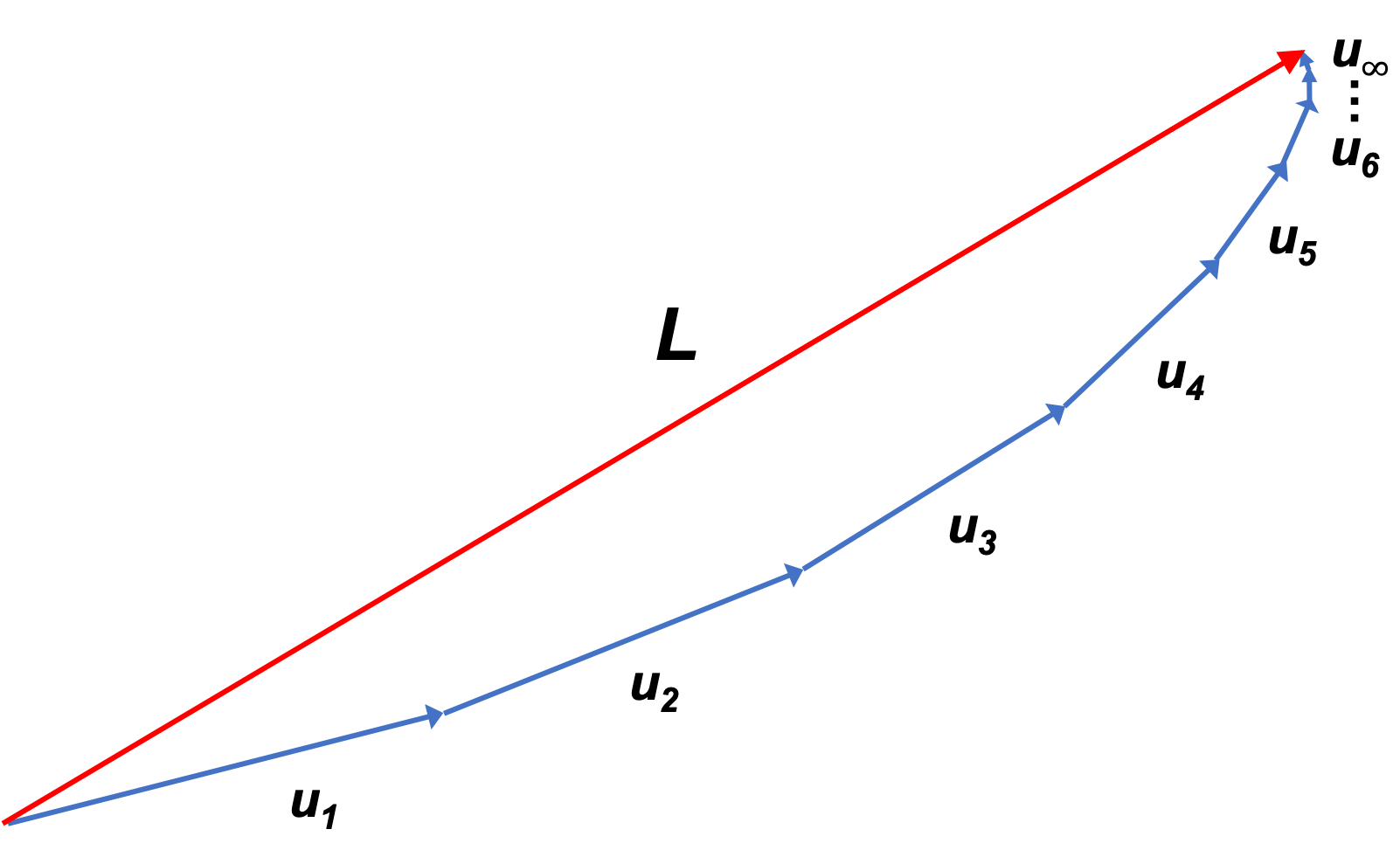
We can also define the completeness of a Hilbert space in terms of a sequence of vectors , where
. Each element
is represented by a series of vectors, which converges absolutely (i.e.
) and converges to an element of
. In other words, the series of vectors in
converges to some limit vector
in
:
Generally, every element of a vector space can be a point, a vector or a function. In quantum mechanics, we are interested in a Hilbert space called the space, where the eigenfunctions of a Hermitian operator are square integrable, i.e.
.
Not to be confused with the completeness of a Hilbert space, the completeness of a set of basis eigenfunctions refers to the property that any eigenfunction of the Hilbert space can be expressed as a linear combination of the basis eigenfunctions. An example is the space, where the set of basis vectors
is complete, with a linear combination of
and
spanning
. In
, the number of basis vectors
may be infinite. If the set of
is complete, we say that it spans
, which is itself complete.
Just as the orthonormal vectors and
form a complete set of basis vectors in the
space, where any vector in
can be expressed as a linear combination of
and
, we postulate the existence of a complete basis set of orthonormal wavefunctions of any Hermitian operator in
.