Inner product space

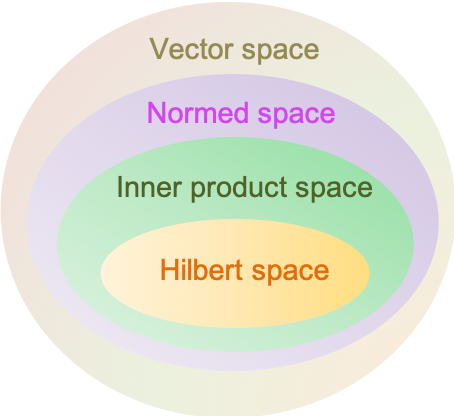
An inner product space is a vector space with an inner product.

An inner product is an operation that assigns a scalar to a pair of vectors $\langle\boldsymbol{\mathit{u}}\vert\boldsymbol{\mathit{v}}\rangle$ , or a scalar to a pair of functions $\langle f\vert g\rangle$ . The way to assign the scalar may be through the matrix multiplication of the pair of vectors, for instance

$\langle\boldsymbol{\mathit{u}}\vert\boldsymbol{\mathit{v}}\rangle=\begin{pmatrix} u_{1}^{*} &u_{2}^{*}& \cdots &u_{N}^{*} \end{pmatrix}\begin{pmatrix} v_1\\v_2 \\ \vdots \\ v_N \end{pmatrix}=\sum_{i=1}^{N}u_{i}^{*}v_i\; \; \; \; \; \; \; \; 3$

or it may be through an integral of the pair of functions:

$\langle f\vert g\rangle=\int_{-\infty}^{\infty}f(x)^{*}g(x)dx$

You may notice that eq3 resembles a dot product. The dot product pertains to vectors in $\mathbb{R}^{3}$ , where $\boldsymbol{\mathit{A}}\cdot\boldsymbol{\mathit{B}}=\sum_{i=1}^{3}A_iB_i$ , which can be extended to $N$ -dimensions, where $\langle\boldsymbol{\mathit{A}}\vert\boldsymbol{\mathit{B}}\rangle=\sum_{i=1}^{N}A_iB_i$ , and to include complex and real functions, $\langle f\vert g\rangle=\int_{-\infty}^{\infty}f(x)^{*}g(x)dx$ . Therefore, an inner product is a generalisation of the dot product.

An inner product space has the following properties:

1. Conjugate symmetry: $\langle f\vert g\rangle=\langle g\vert f\rangle^{*}$
2. Additivity: $\langle f+g\vert h\rangle=\langle f\vert h\rangle+\langle g\vert h\rangle$
3. Positive semi-definiteness: $\langle f\vert f\rangle\geq 0$ , with $\langle f\vert f\rangle= 0$ if $f=0$

Question

i) Why is the inner product space positive semi-definite? ii) Show that orthogonal vectors are linearly independent.

Answer

i) A general vector space of $\langle\boldsymbol{\mathit{a}}\vert\boldsymbol{\mathit{a}}\rangle$ can be positive or negative. The inner product space is defined such that $\langle f\vert f\rangle\geq 0$ , with $\langle f\vert f\rangle= 0$ if $f=0$ , which is useful in quantum mechanics.

ii) Let the set of vectors $\left \{ \boldsymbol{\mathit{v_k}} \right \}$ in eq1 be orthogonal vectors. The dot product of eq1 with $\boldsymbol{\mathit{v_i}}$ gives $c_i\boldsymbol{\mathit{v_i}}\cdot\boldsymbol{\mathit{v_i}} =c_i\left |\boldsymbol{\mathit{v_i}} \right |^{2}=0$ . Since the magnitudes of orthogonal vectors are non-zero, $c_i=0$ . Hence, orthogonal vectors are linearly independent.

Two functions (or two vectors) are orthogonal if $\langle f\vert g\rangle= 0$ . Elements of a set of basis functions are orthonormal if $\langle \phi_i\vert \phi_j\rangle=\delta_{ij}$ where

$\delta_{ij}= \{\; \begin{matrix} 1 & for\; \; i=j\\ 0 & for\; \; i\neq j \end{matrix}$

In other words, two functions (or two vectors) are orthonormal if they are orthogonal and normalised.

Finally, the norm (or length) of a vector $\boldsymbol{\mathit{u}}$ is denoted by $\left \|\boldsymbol{\mathit{u}}\right \|$ and is defined as $\left \|\boldsymbol{\mathit{u}}\right \|=\sqrt{\langle\boldsymbol{\mathit{u}}\vert\boldsymbol{\mathit{u}}\rangle}=\sqrt{\left |\boldsymbol{\mathit{u}}\right |\left |\boldsymbol{\mathit{u}}\right |cos\: 0^{\circ} }=\left |\boldsymbol{\mathit{u}}\right |$ . With this association of inner product and the length of a vector, we can establish the relationship between inner product $\langle\boldsymbol{\mathit{u}}\vert\boldsymbol{\mathit{v}}\rangle$ and the Euclidean distance $d(\boldsymbol{\mathit{u}},\boldsymbol{\mathit{v}})$ between 2 vectors $\boldsymbol{\mathit{u}}$ and $\boldsymbol{\mathit{v}}$ . Using the $\mathbb{R}^{2}$ space as an example, where $\boldsymbol{\mathit{u}}=\begin{pmatrix} 6\\9 \end{pmatrix}$ and $\boldsymbol{\mathit{v}}=\begin{pmatrix} 3\\5 \end{pmatrix}$ , we have

$d(\boldsymbol{\mathit{u}},\boldsymbol{\mathit{v}})=\left \|\boldsymbol{\mathit{u}}-\boldsymbol{\mathit{v}}\right \|=\sqrt{\langle\boldsymbol{\mathit{u}}- \boldsymbol{\mathit{v}}\vert\boldsymbol{\mathit{u}}- \boldsymbol{\mathit{v}}\rangle}=\sqrt{\langle\begin{pmatrix} 3\\4 \end{pmatrix}\vert \begin{pmatrix} 3\\4 \end{pmatrix}\rangle}$

$=\sqrt{\begin{pmatrix} 3 &4 \end{pmatrix}\begin{pmatrix} 3\\4 \end{pmatrix}}=5$

Inner product space

Question

Answer

Next article: vector subspace and eigenspace

Previous article: vector space of functions

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply