Hund’s rules, created by Friedrich Hund in 1927, consist of three principles used to identify the lowest energy term symbol of a given atomic configuration. They are:
- The term symbol with the highest multiplicity represents state(s) with the lowest energy.
This is due to the spin correlation between spin angular momenta of electrons, where the expectation value of the distance between a pair of electrons in the triplet state is greater than the expectation value of the distance between a pair of electrons in the singlet state. Consequently, there is less electron-electron repulsion for the triplet state (higher multiplicity) than for the singlet state.
- For a particular multiplicity, the term symbol with the highest
is lowest in energy.
This results from the Coulomb interaction between orbital angular momentum of a pair of electrons, where electrons orbiting in the same direction meet less often than when they are orbiting in opposite directions. This implies that . Since the individual angular momentum of each electron orbiting in the same direction adds vectorially to give a higher total angular momentum (and hence a higher value of the quantum number
) than electrons orbiting in opposite directions, the term symbol with the highest
is lowest in energy.
- Generally, for a particular term describing an atom with a less than half-filled outermost subshell, the term symbol with the lowest
is lowest in energy. If the subshell is more than half-filled, the term symbol with the highest
is lowest in energy.
This is because the value of in eq289, which is empirically evaluated, generally changes from positive to negative when the subshell is more than half-filled.

Question
What about a half-filled subshell?
Answer
Examples of electron configuration of half-filled subshells are p3 and d5, with terms 4S and 6S respectively and corresponding levels of 4S3/2 and 6S5/2 respectively. Since the level of a half-filled subshell is described by only one term symbol, which always has the highest multiplicity of all microstates of the associated electron configuration, it is always lowest in energy. In other words, no rules are needed to determine the lowest energy term symbol of electron configurations like p3 and d5.
Since term symbols are based on Russell-Saunders coupling, where we assume that spin-spin coupling > orbit-orbit coupling > spin-orbit coupling, the three rules are applied in the above order (from rule 1 to rule 3) when we determine the lowest energy term symbol of a given configuration of an atom. The ground states of carbon and nitrogen are therefore 3P0 and 4S3/2 respectively.
Hund’s rules are often stated as a single rule at introductory courses, with the rule being: electrons occupy the orbitals of a subshell singly and in parallel before pairing up. This statement is another way to state the first rule, which is the most dominant. Using the example of the shell of the ground state of carbon, the two electrons in the 2p orbitals are parallel because of the first rule.
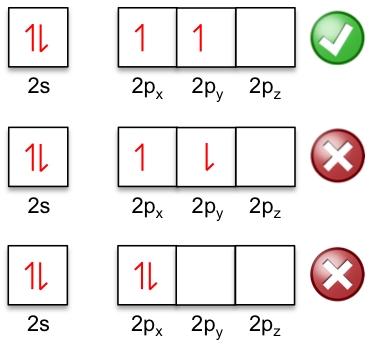

Question
Why are the two electrons in the 2s orbital anti-parallel?
Answer
This is also a consequence of the first rule, where the spatial wavefunction associated with a triplet state is . If
, and
and
, which implies that there is zero probability of finding the two parallel electrons at the same point.