Modern atomic structure

The earlier models of the atom were constructed using classical mechanics. When Niels Bohr introduced his model of the atom, he not only utilised Newtonian mechanics in his derivation but also incorporated the Planck relation E = hv, which was conceived a decade earlier by Max Planck, a German physicist.

In 1900, Planck was trying to develop a formula to describe the radiation spectrum of a black body when he suggested that electromagnetic radiation is a form of energy that is quantised. The significance of this concept eventually led to development of quantum theory, with Planck being regarded as the father of quantum mechanics.

Quantum mechanics is key to the elucidation of the modern structure of an atom, where electrons are no longer perceived as orbiting in defined paths around the nucleus. Instead, an atom is represented by equations that describe the probability distribution of electrons in space, giving rise to a nucleus that is surrounded by an electron cloud (see below diagram).

In the modern interpretation of the atomic structure, electrons are distributed in an atom in specific energy states that are characterised by mathematical functions known as orbitals. The maximum number of electrons that an orbital can accommodate is two (see this article for details). Orbitals with similar shapes form a sub-shell (characterised by a unique set of (n, l), e.g. p_x, p_y and p_z forms the sub-shell p), and sub-shells with the same energy in the absence of an external magnetic field, constitute a shell (e.g. 2s and 2p sub-shells constitute the shell n = 2). Diagrammatically, we can describe the energy states as follows:

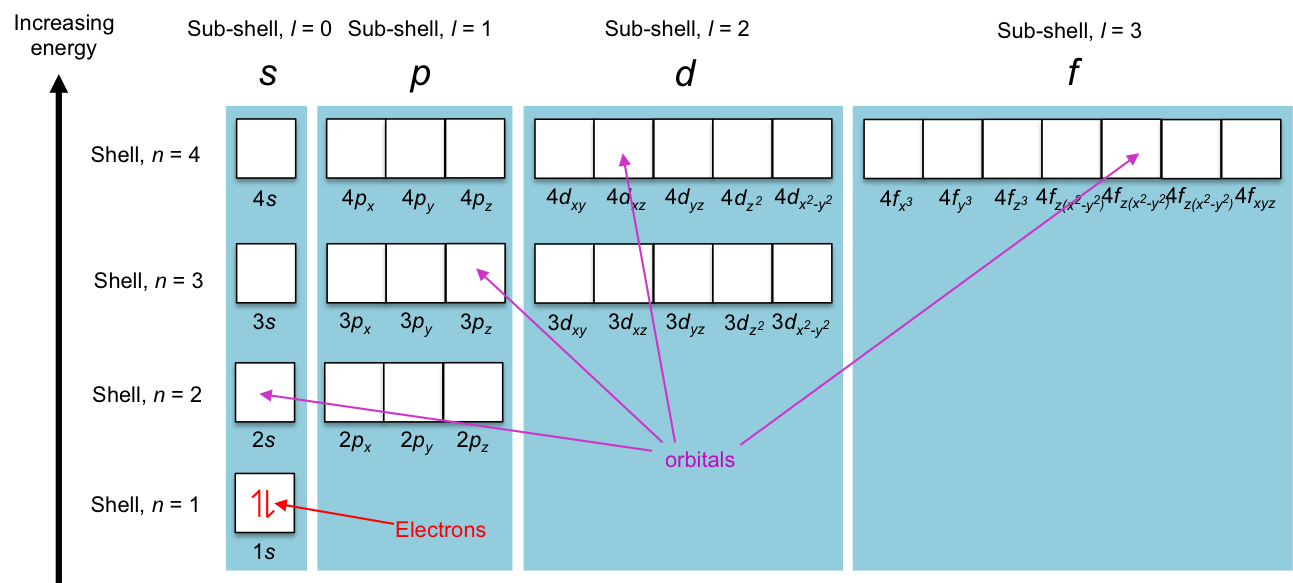
Mathematically, the energy states are defined by four quantum numbers, n, ,  and m_s, as shown in the table below.

Quantum numbers			Details	Example
Symbol	Name	Values
n	Principal		Each value of n refers to a shell	n = 1 and n = 2 are the 1st shell and 2nd shell of an atom respectively.
	Angular		Each value of refers to a sub-shell where	For the 1st shell (n = 1), , i.e. the 1st shell consists only of the sub-shell s. For the 2nd shell (n = 2), , i.e. the 2nd shell consists of two sub-shells, s and p.
	Magnetic	with a total of values	Each value of refers to the orientation of an orbital in a sub-shell. The total number of values in a sub-shell also refers to the total number of orbitals in that sub-shell.	For the 1st shell (n = 1), , and , with a total of one value, i.e. there is only one orbital in the 1st shell. For the s sub-shell in the 2nd shell, with a total of one  value, i.e. there’s only 1 orbital in the s sub-shell with a single orientation. For the p sub-shell in the 2nd shell, with a total of three values, i.e. 3 orbitals in the p sub-shell, with each orbital having a distinct orientation.
	Spin magnetic	or	Each value of refers to the spin orientation of an electron.	refers to a spin-up electron, while  refers to a spin-down electron

In other words, the four quantum numbers describe the energy state of an electron in an atom. The numbers are a result of many scientists’ work that were done during the early 1900s. Some of these experiments and theories that contributed to the development of quantum mechanics are listed in the table below.

Year	Work	Scientist
1900	Planck’s law	Max Planck
1905	Photoelectric effect	Albert Einstein
1924	de Broglie’s hypothesis	Louis de Broglie
1925	Schrodinger equation	Erwin Schrodinger
1925	Pauli exclusion principle	Wolfgang Pauli
1926	Born interpretation	Max Born
1920-1930	Aufbau principle, Madelung’s rule and Hund’s rule	Niels Bohr, Wolfgang Pauli, Erwin Madelung, Friedrich Hund
1927	Heisenberg’s uncertainty principle	Werner Heisenberg

We shall elaborate on the above in the following articles.

 

 

Next article: Black body radiation

Previous article: Classical atomic theory

Content page of intermediate quantum chemistry

Content page of intermediate chemistry

Main content page