Atomic orbital energies are eigenvalues of the Hartree-Fock equations. These eigenvalues are expressed by eq148, and are based on a specific state of the atom. As illustrated in the article on the analytical solution of the Hartree-Fock method for the ground state of Li, we can theoretically compute for any occupied orbital of an atom. For example,
of the 2p orbital of Li can be determined using the excited electron configuration state of 1s22p1. However, if we want to determine the energies of unoccupied orbitals of an atom in its ground state, we would have to use the Hartree-Fock-Roothaan method, where the basis set includes a linear combination of the 1s, 2s and 2p wavefunctions. In general,
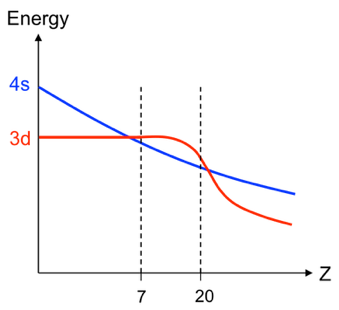
for atoms with
to
are depicted in the diagram below.

For atoms with , their 4s orbital energies lie below their respective 3d orbital energies (see diagram below). An example is the atom
with the ground state electron configuration [Ar]4s1. This implies that the theoretical ground state energy of
is closer to the experimental value when we use a 4s Slater-type orbital rather than a 3d Slater-type orbital for computing
.
With that in mind, one may conclude that the ground state electron configuration of Sc is [Ar]3d3. However, it is [Ar]3d14s2. This is because the orbital energies and
for [Ar]3d3 are different from those for [Ar]3d14s2 (refer to eq148), even though
for both configurations. For example,
for the electron configurations [Ar]3d14s2 and [Ar]3d24s2 are (in Hartree units)
and
respectively, where .
In short, the Hartree-Fock computation using the electron configuration of [Ar]3d14s2 gives a ground state energy that is closest to experimental values. Qualitatively, we rationalise the above with the fact that 3d orbitals are smaller in size compared to the 4s orbitals. Electrons occupying 3d orbitals therefore experience greater repulsions than electrons residing in 4s orbitals, with the order of increasing repulsion being:
where V is the potential energy due to repulsion.
Therefore, to determine the stability of an atom in the ground state, we need to consider the net effect of the relative energies of 4s/3d orbitals and the repulsion of electrons. Calculations for the overall energies of Sc show that
