Analytical solution of the energy equation for Li using the Hartree-Fock method

The analytical solution of the energy equation for Li involves finding analytical expressions for all terms in eq94 using one-electron trial wavefunctions. Guess values are used for the variables in all the wavefunctions except one, e.g. $\phi_1(\boldsymbol{\mathit{ r}}_1)$ . Eq94 is then minimised to obtain the solutions for E and $\phi_1(\boldsymbol{\mathit{ r}}_1)$ . The process is repeated until E and all $\phi_i(\boldsymbol{\mathit{ r}}_i)$ become invariant.

After removing $K_{12}$ and $K_{23}$ due to spin orthogonality from eq94, we have

$E=H_1+H_2+H_3+J_{12}+J_{13}+J_{23}-K_{13}\;\;\;\;\;\;\;\;(113)$

where
$H_i=\int\phi_i^*(\boldsymbol{\mathit{r}}_i)\left(-\frac{1}{2}\nabla_i^2-\frac{Z}{r_i}\right)\phi_i(\boldsymbol{\mathit{r}}_i)d\boldsymbol{\mathit{r}}_i$
$J_{ij}=\int\int\phi_i^*(\boldsymbol{\mathit{r}}_i)\phi_j^*(\boldsymbol{\mathit{r}}_j)\frac{\phi_i(\boldsymbol{\mathit{r}}_i)\phi_j(\boldsymbol{\mathit{r}}_j)}{r_{ij}}d\boldsymbol{\mathit{r}}_id\boldsymbol{\mathit{r}}_j$
$K_{ij}=\int\int\phi_i^*(\boldsymbol{\mathit{r}}_i)\phi_j^*(\boldsymbol{\mathit{r}}_j)\frac{\phi_j(\boldsymbol{\mathit{r}}_i)\phi_i(\boldsymbol{\mathit{r}}_j)}{r_{ij}}d\boldsymbol{\mathit{r}}_id\boldsymbol{\mathit{r}}_j$

Our computation employs the following assumptions:

The ground state of Li is described by a single Slater determinant.
Eq113 is minimised iteratively via the restricted open-shell method, where the 1s orbital is doubly occupied with $\phi_1=\phi_2=\sqrt{\frac{\zeta_1^3}{\pi}}e^{-\zeta_1r}$ , while the 2s orbital is singly occupied. Therefore, we can substitute eq56 in eq113, where $\alpha=\beta=\zeta_1$ , to give

$E=\zeta_1^2-\frac{27}{8}\zeta_1+H_3+J_{13}+J_{23}-K_{13}\;\;\;\;\;\;\;\;(114)$

The 2s Slater-type orbital $\phi_3^{' }$ is derived via the Gram-Schmidt process, as the generic 2s Slater-type orbital is not orthogonal to the 1s Slater-type orbital.

Question

Using the normalised 1s Slater-type orbital $\phi_1=\sqrt{\frac{\zeta_1^3}{\pi}}e^{-\zeta_1r}$ and the un-normalised generic 2s Slater-type orbital $\chi_3=re^{-\zeta_3r}$ , derive $\phi_3^{' }$ via the Gram-Schmidt process.

Answer

With reference to eq111, we have

$\phi_3^{' }=N'\left(\chi_3-\frac{\int\chi_3\phi_1d\tau}{\int\phi_1\phi_1d\tau}\phi_1\right)=N'\left(\chi_3-\int\chi_3\phi_1d\tau\phi_1\right)$

where N’ is the normalisation constant.

Substituting $\phi_1$ and $\chi_3$ in the above equation and integrating using the identity $\int_0^{\infty}x^ne^{-mx}dx=\frac{n!}{m^{n+1}}$ , and then normalising and rearranging the result, we have

$\phi_3^{' }=N\phi_3-M\phi_1\;\;\;\;\;\;\;\;(116)$

where
$N=\sqrt{\frac{(\zeta_1+\zeta_3)^8}{(\zeta_1+\zeta_3)^8-192\zeta_1^3\zeta_3^5}}$
$\phi_3=\sqrt{\frac{\zeta_3^5}{3\pi}re^{-\zeta_3r}$
$M=\frac{8}{(\zeta_1+\zeta_3)^4}\sqrt{\frac{3\zeta_1^3\zeta_3^5(\zeta_1+\zeta_3)^8}{(\zeta_1+\zeta_3)^8-192\zeta_1^3\zeta_3^5}}$

Let’s evaluate the remaining terms in eq114, beginning with $H_3=\int\phi_3^{'*}\left(-\frac{1}{2}\nabla^2-\frac{Z}{r}\right)\phi_3^{'}d\tau$ . Substituting eq116 in $H_3$ and integrating,

$H_3=N^2\left(\frac{\zeta_3^2}{6}-\frac{\zeta_3Z}{2}\right)+NM\frac{\sqrt{48\zeta_1^7\zeta_3^5}}{(\zeta_1+\zeta_3)^4}-\frac{NM}{(\zeta_1+\zeta_3)^3}\sqrt{\frac{64\zeta_1^5\zeta_3^5}{3}}$ $+\frac{NMZ}{(\zeta_1+\zeta_3)^3}\sqrt{\frac{256\zeta_1^3\zeta_3^5}{3}}+NM\frac{\sqrt{48\zeta_1^3\zeta_3^9}}{(\zeta_1+\zeta_3)^4}-\frac{NM}{(\zeta_1+\zeta_3)^3}\sqrt{\frac{256\zeta_1^3\zeta_3^7}{3}}$ $+\frac{NM}{(\zeta_1+\zeta_3)^2}\sqrt{\frac{16\zeta_1^3\zeta_3^5}{3}}+M^2\frac{\zeta_1^2}{2}-M^2Z\zeta_1\;\;\;\;\;\;\;\;(119)$

Next, we evaluate $J_{13}$ , which is equal to $J_{23}$ . Substituting eq116 and eq47 in $J_{13}=\int_0^{\infty}\phi_1^*(\boldsymbol{\mathit{r}}_1)\phi_3^{'*}(\boldsymbol{\mathit{r}}_3)\frac{\phi_1(\boldsymbol{\mathit{r}}_1)\phi_3^{' }(\boldsymbol{\mathit{r}}_3)}{r_{13}}d\tau$ and integrating (refer to the integration procedure in this article), we have

$J_{13}=J_{23}=\frac{N^2\zeta_3}{2}-\frac{N^2\zeta_3^5}{2(\zeta_1+\zeta_3)^4}-\frac{N^2\zeta_1\zeta_3^5}{(\zeta_1+\zeta_3)^5}-\frac{2NM}{(\zeta_1+\zeta_3)^3}\sqrt{\frac{64\zeta_1^3\zeta_3^5}{3}}$ $+\frac{2NM}{(3\zeta_1+\zeta_3)^3}\sqrt{\frac{64\zeta_1^3\zeta_3^5}{3}}+\frac{NM\sqrt{768\zeta_1^5\zeta_3^5}}{(3\zeta_1+\zeta_3)^4}+\frac{5}{8}M^2\zeta_1\;\;\;\;\;\;\;\;(129)$

Finally, we evaluate $K_{13}=\int_0^{\infty}\phi_1^*(\boldsymbol{\mathit{r}}_1)\phi_3^{'*}(\boldsymbol{\mathit{r}}_3)\frac{\phi_1(\boldsymbol{\mathit{r}}_3)\phi_3^{ '}(\boldsymbol{\mathit{r}}_1)}{r_{13}}d\tau$ . Referencing the steps in integrating $J_{13}$ , we have

$K_{13}=\frac{44N^2\zeta_1^3\zeta_3^5}{(\zeta_1+\zeta_3)^7}-\frac{NM}{(\zeta_1+\zeta_3)^3}\sqrt{\frac{64\zeta_1^3\zeta_3^5}{3}}+\frac{NM}{(3\zeta_1+\zeta_3)^3}\sqrt{\frac{64\zeta_1^3\zeta_3^5}{3}}$ $+NM\frac{\sqrt{192\zeta_1^5\zeta_3^5}}{(3\zeta_1+\zeta_3)^4}-NM\frac{\sqrt{192\zeta_1^5\zeta_3^5}}{(\zeta_1+\zeta_3)^4}+\frac{NM}{(\zeta_1+\zeta_3)^4}\frac{\sqrt{3072\zeta_1^9\zeta_3^5}}{(3\zeta_1+\zeta_3)^2}$ $+\frac{NM}{\sqrt 3(\zeta_1+\zeta_3)^3}\frac{\sqrt{16384\zeta_1^9\zeta_3^5}}{(3\zeta_1+\zeta_3)^3}+\frac{NM}{(\zeta_1+\zeta_3)^2}\frac{\sqrt{3072\zeta_1^9\zeta_3^5}}{(3\zeta_1+\zeta_3)^4}+\frac{5}{8}M^2\zeta_1\;\;\;\;\;\;\;\;(142)$

Substituting eq119, eq129, eq142 and the atomic number $Z=3$ in eq114, we have the analytical expression of E, which is used in an iterative algorithm to determine the ground state of Li. The procedure involves setting up an iterative table in Excel as follows:

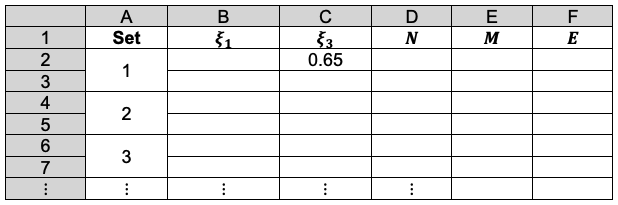
Cell C2 is the initial guess value of $\zeta_3$ . Cell F2 contains the entire formula of the analytical expression of E, with links to B1, C1, D1 and E1. Cell D2 and E2 contain the formulae of N and M respectively, with links to B1 and C1. The formulae for B3, D3 and E3 are ‘=B2’, ‘=D2’ and ‘=E2’ respectively. To compute the first iteration set, we employ the Excel Solver application to minimise F2 with respect to B2, with the following settings:

Set objective: F2
To: Min
By changing variable cells: B2
Selecting a solving method: GRG Nonlinear

We then solve for F3 by changing the ‘Set objective’ field and ‘By changing variable cells’ field to D3 and C3 respectively. This procedure is repeated for subsequent iteration sets until the values of $\zeta_1$ and $\zeta_3$ are invariant up to seven decimal points.

The results are as follows:

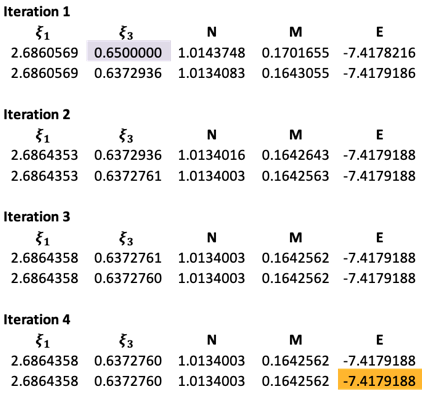
The final theoretical value of $E=-7.4179188$ has a deviation of about 0.80% versus the experiment data of the ground state of Li.

Analytical solution of the energy equation for Li using the Hartree-Fock method

Question

Answer

Next article: Analytical solution of the Hartree-Fock method for Be, B and C

Previous article: Exchange integral

Content page of computational chemistry

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply