Group

A group is a set, together with a chosen binary operation, that satisfies the properties of closure, identity, inverse and associativity as follows:

1. Closure: if $a$ and $b$ are elements of the group $G$ , then $c=a*b$ is also an element of $G$ .
2. Identity: there exists an element called the identity, which is denoted by $e$ , such that $e*k=k*e=k$ for $k\in G$ .
3. Inverse: every element $a$ in $G$ has an inverse $a^{-1}$ , which is itself an element of $G$ , such that $a^{-1}*a=a*a^{-1}=e$ .
4. Associativity: $(a*b)*c=a*(b*c)$ for all $a,b,c\in G$ .

Consider the set $A=\{0,1,2,3\}$ under the binary operation of addition mod 4. It is a group because it satisfies the four properties mentioned above. For example, the element 0 is the identity, since $a+0=0+a=a$ , where $a\in A$ . As for inverses, $0^{-1}=0$ , because $0^{-1}+0$ gives the identity. Similarly, $1^{-1}=3$ , $2^{-1}=2$ and $3^{-1}=1$ . The closure and associativity properties can be easily verified.

Question

What is addition mod 4 for the set $A=\{0,1,2,3\}$ ?

Answer

It means that if the sum of two elements of the set is greater than 3, then we divide the result by 4 (called the modulus) and take the remainder as the answer. For example, $0+3=3$ , $0+4=0$ and $2+3=1$ .

Similarly, the set $B=\{1,3,5,7\}$ under the binary operation of multiplication mod 8 is a group. In this case, if the product of two elements of $B$ is greater than 7, we divide the result by 8 and take the remainder as the answer. All possible binary operations and answers can be presented in the form of a multiplication table as follows:

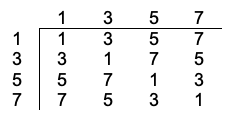
where the left operand and right operand of the binary operation $a*b$ are listed in the top row and the leftmost column respectively.

Clearly, the multiplication of integers is associative. From the multiplication table, we can validate the closure property of $B$ , authenticate that 1 is the identity element and determine that the inverse of an element is the element itself. The associativity property is also easily verified separately.

Question

Is the set $A=\{0\}$ under the binary operation of multiplication a group?

Answer

Yes, it is a trivial group with only one element.

If the results of all binary operations of a group are independent of the order of the operands (i.e., $a*b=b*a$ ), the group is said to be Abelian. Both groups $A$ and $B$ mentioned above are examples of Abelian groups.

The order of a group $G$ , denoted by $\vert G\vert$ , is the number of elements in $G$ . For example, $\vert G\vert=4$ for both $A$ and $B$ . The order of an element $g$ of a group $G$ under the binary operation of multiplication, denoted by $\vert g\vert$ , is the smallest value of $n$ such that $g^n=e$ . For example, the order of the all elements in the group $B$ is 2.

Finally, some useful properties of a group can be inferred from the main properties of closure, identity, inverses and associativity. Two such inferred properties are:

Cancellation

(Statement) If $ab=ac$ , then $b=c$ for all $a$ in the group $G$ . In other words, $a$ is “cancellable”.

According to the inverses property of a group, if $a\in G$ , there exists a unique $a^{-1}$ , where $a^{-1}\in G$ . The proof for the cancellation theorem then involves left-multiplying $ab=ac$ by $a^{-1}$ and using the associativity and identity properties:

$a^{-1}(ab)=a^{-1}(ac)\implies(a^{-1}a)b=(a^{-1}a)c\implies eb=ec\implies b=c$

Question

Proof the uniqueness of inverses in a group, i.e. for each $a\in G$ , there is a unique element $b$ such that $ab=ba=e$ .

Answer

Suppose $a$ has two inverses $b$ and $c$ . Then $ab=e=ac$ or $ab=ac$ . By cancellation, $b=c$ .

Rearrangement theorem

(Statement) Let $G=\{e,a,b,\cdots,n\}$ and $k\in G$ . Suppose we multiply each element of $G$ by $k$ to form a new group $G'$ , where $G'=Gk=\{ek,ak,bk,\cdots,nk\}$ . Then, $G'$ contains each element of $G$ once and only once. In other words, $G'=G$ .

This theorem is proven by contradiction. Suppose two elements of $G'$ are equal, where $ak=bk$ . By cancellation, we have $a=b$ , which contradicts the definition that a group is a set, which is a collection of different elements. However, if $k\neq e$ , the order of elements in $G'$ may not be the same as that in $G$ , and thus the term ‘rearrangement’.

Question

Answer

Question

Answer

Question

Answer

Next article: Symmetry element and symmetry operation

Previous article: Binary operation

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply