Schur’s second lemma

Schur’s second lemma describes the restrictions on a matrix that commutes with elements of two distinct irreducible representations, which may have different dimensions.

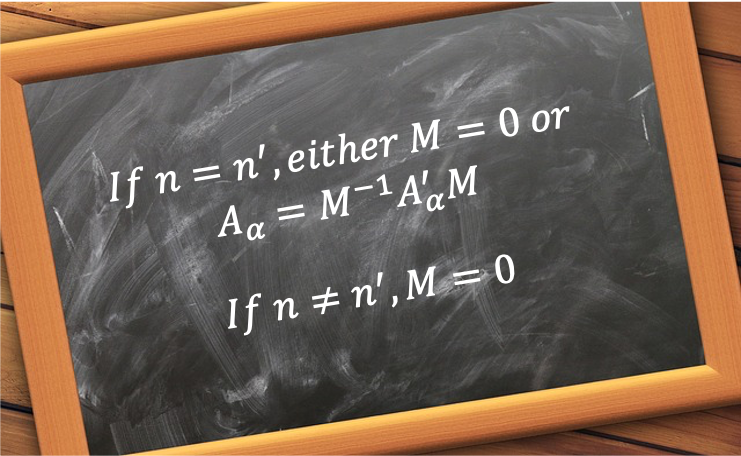
Consider an arbitrary matrix $M$ and two irreducible representations of a group, $A_{\alpha}$ of dimension $n$ and $A_{\alpha}'$ of dimension $n'$ , such that

$MA_{\alpha}=A_{\alpha}'M\;\;\;\;\;\;\;\;10$

where $\alpha=1,2,\cdots,\vert G\vert$ .

Taking the conjugate transpose of eq10 and using the matrix identity $(AB)^{\dagger}=B^{\dagger}A^{\dagger}$ , we have $A_{\alpha}^{\dagger}M^{\dagger}=M^{\dagger}A_{\alpha}^{'\dagger}$ . As every element of a representation of a group can be expressed as a unitary matrix $U$ via a similarity transformation without any loss of generality, and as $U^{\dagger}=U^{-1}$ ,

$A_{\alpha}^{-1}M^{\dagger}=M^{\dagger}A_{\alpha}^{'-1}\;\;\;\;\;\;\;\;11$

Since the inverse property of a group states that $A_{i}^{-1}=A_{j}$ and $A_{i}^{'-1}=A_{j}'$ , we can express eq10 as

$MA_{\alpha}^{-1}=A_{\alpha}^{'-1}M\;\;\;\;\;\;\;\;12$

Multiplying eq11 on the left by $M$ and using eq12, we have $MA_{\alpha}^{-1}M^{\dagger}=MM^{\dagger}A_{\alpha}^{'-1}$ and therefore $A_{\alpha}^{'-1}(MM^{\dagger})=(MM^{\dagger})A_{\alpha}^{'-1}$ , which implies that $MM^{\dagger}$ commutes with all elements of an irreducible representation of $G$ . With reference to Schur’s first lemma,

$MM^{\dagger}=cI\;\;\;\;\;\;\;\;13$

where $c$ is a constant and $I$ is the identity matrix.

If we multiply eq11 on the right by $M$ and repeat the steps above, we have

$M^{\dagger}M=cI\;\;\;\;\;\;\;\;14$

Let’s consider the following cases for eq13:

Case 1: $n=n'$

Let the $(i,k)$ -th entry of $M$ be $m_{ik}$ . If $n=n'$ , we can rewrite eq13 in terms of matrix entries: $\sum_{k=1}^nm_{ik}m^*_{ik}=c\delta_{mn}\implies \sum_{k=1}^n\vert m_{ik}\vert^2=c\delta_{mn}$ . If $c=0$ , we have $\sum_{k=1}^n\vert m_{ik}\vert^2=0$ , which implies that $M$ is the zero matrix because $m_{ik}=0$ for all $i,k$ .

Combining eq13 and eq14, we have $MM^{\dagger}=cI=M^{\dagger}M$ or $M(\frac{1}{c}M^{\dagger})=I=(\frac{1}{c}M^{\dagger})M$ . This implies that $M^{-1}=\frac{1}{c}M^{\dagger}$ exists if $c\neq 0$ . We can therefore rewrite eq10 as $A_{\alpha}=M^{-1}A_{\alpha}'M$ , which is a similarity transformation if $c\neq 0$ .

Case 2: $n\neq n'$

If $n\neq n'$ , the arbitrary matrix (denoted by $M'$ ) is an $n'\times n$ matrix with reference to eq10. Suppose $n<n'$ ; we have:

$M'=\begin{pmatrix}m_{11}&m_{12}&\cdots&m_{1n}\\m_{21}&m_{22}&\cdots&m_{2n}\\\vdots&\vdots&\ddots&\vdots\\m_{n'1}&m_{n'2}&\cdots&m_{n'n}\end{pmatrix}$

If we enlarge $M'$ to form an $n'\times n'$ matrix $N$ with the additional elements equal to zero, we have

$N=\begin{pmatrix}m_{11}&m_{12}&\cdots&m_{1n}&0&\cdots&0\\m_{21}&m_{22}&\cdots&m_{2n}&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots\\m_{n'1}&m_{n'2}&\cdots&m_{n'n}&0&\cdots&0\end{pmatrix}\;\;\;N^{\dagger}=\begin{pmatrix}m_{11}^*&m_{21}^*&\cdots&m_{n'1}^*\\m_{12}^*&m_{22}^*&\cdots&m_{n'2}^*\\\vdots&\vdots&\ddots&\vdots\\m_{1n}^*&m_{2n}^*&\cdots&m_{n'n}^*\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{pmatrix}$

Due to the zeroes, $NN^{\dagger}=MM^{\dagger}=cI$ . Taking the determinants,

$\vert NN^{\dagger}\vert=\vert cI\vert$

Using the determinant identities $\vert AB\vert=\vert A\vert\vert B\vert$ , $\vert cA\vert=c^n\vert A\vert$ and $\vert I\vert=1$ , we have

$\vert N\vert\vert N^{\dagger}\vert=c^n$

Since one of the columns of $N$ is zero, $\vert N\vert=0$ . So, $c=0$ , which implies that $M$ must be a zero matrix according to the results of case 1.

Finally, we can summarise Schur’s second lemma as follows:

Given an arbitrary matrix $M$ and two irreducible representations, $A_{\alpha}$ of dimension $n$ and $A_{\alpha}'$ of dimension $n'$ , where $MA_{\alpha}=A_{\alpha}'M$ , then

1. if $n=n'$ , either $M=0$ or the representations are related by a similarity transformation, i.e. equivalent representations.
2. If $n\neq n'$ , $M=0$ .

Schur’s second lemma

Next article: Great orthogonality theorem

Previous article: Schur’s first lemma

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply