A unitary representation of a group consists of elements that are unitary matrices.
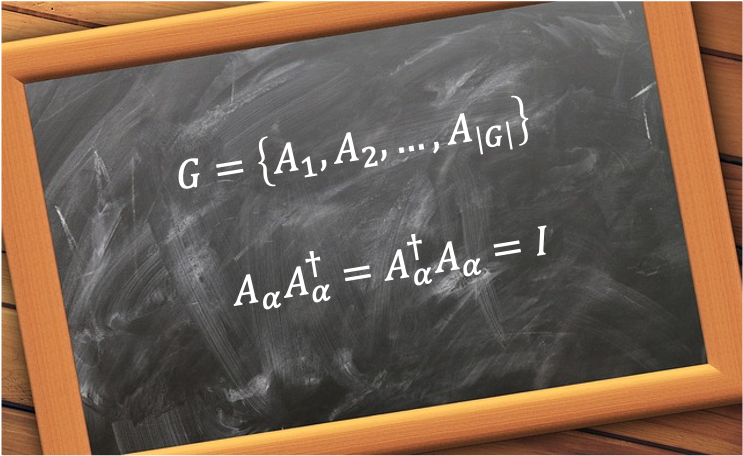
Every representation of a group can be described in terms of unitary matrices. Specifically, matrices of a representation of a group can be expressed as unitary matrices via a common similarity transformation without any loss of generality. The proof is as follows:
Consider a group 
, where each element is an 
matrix. Let’s construct a new matrix 
out of the elements of 
, where 
.
Question
Proof the matrix identity ^{\dagger}=B^{\dagger}A^{\dagger})
.
Answer
_{ij}^{\dagger}=(A^*B^*)_{ij}^{T}=(A^*B^*)_{ji}=\sum_kA_{jk}^*B_{ki}^*\\=\sum_k(B^{*T})_{ik}(A^{*T})_{kj}=(B^{\dagger}A^{\dagger})_{ij})
Using the identity mentioned above,
^{\dagger}=\sum_{\alpha=1}^{\vert G\vert}A_{\alpha}A_{\alpha}^{\dagger}=H)
Therefore, is a Hermitian matrix, which can be diagonalised by a unitary matrix 
, i.e. 
. Using 
and the above identity again, we have,
(U^{\dagger}A_{\alpha}^{\dagger}U)=\sum_{\alpha=1}^{\vert G\vert}(U^{\dagger}A_{\alpha}U)(U^{\dagger}A_{\alpha}U)^{\dagger})
or
where 
.
The diagonal elements of 
are _{kj}(\tilde A_{\alpha}^{\dagger})_{jk}=\sum_{j=1}^{n}(\tilde A_{\alpha})_{kj}(\tilde A_{\alpha})^*_{kj}=\sum_{j=1}^{n}\vert(\tilde A_{\alpha})_{kj}\vert^2\geq 0)
and hence, the diagonal elements of 
are _{kj}\vert^2)
. Moreover, one of the elements 
of is the identity matrix, with 
and 
. So, _{kj}\vert^2+\sum_{j=1}^n\vert(\tilde A_{2})_{kj}\vert^2+\cdots+1+\cdots+\sum_{j=1}^n\vert(\tilde A_{\vert G\vert})_{kj}\vert^2> 0)
.
Let 
and 
be
where 
, 
and 
.
Consider a new set of matrices 
, where 
. Since 
is diagonal and 
is real and positive, we have ^{\dagger}=D^{\pm 1/2})
. Therefore, ^{\dagger}=D^{1/2}\tilde A_{\alpha}^{\dagger}D^{-1/2})
and
(D^{1/2}\tilde A_{\alpha}^{\dagger}D^{-1/2})=D^{-1/2}\tilde A_{\alpha}D\tilde A_{\alpha}^{\dagger}D^{-1/2})
Substitute eq1 in the above equation and changing the dummy index from 
to 
,
^{\dagger}D^{-1/2}\;\;\;\;\;\;\;\;2)
Question
Show that the set 
is also a representation of .
Answer
If the set is also a representation of , its elements must multiply according to the multiplication table of . Since, , we have (U^{\dagger} A_{j}U)=U^{\dagger}A_iA_jU=U^{\dagger}A_kU=\tilde A_k)
. The third equality ensures that the closure property of is satisfied for the set 
and hence the set . In other words, the elements of 
multiply according to the multiplication table of .
If 
, then (U^{\dagger}EU)=U^{\dagger}A_iU)
. Since, 
, the only possibility is that 
for 
. Therefore, the set has the identity element.
To show that each has an inverse, we have
(U^{\dagger} A_{\alpha}U)^{-1}=(U^{\dagger} A_{\alpha}U)(U^{-1} A_{\alpha}U)^{-1}\\=U^{\dagger}A_{\alpha}UU^{-1}A_{\alpha}^{-1}U=U^{\dagger}A_{\alpha}A_{\alpha}^{-1}U=U^{\dagger}U=I)
Finally, the associativity property of the group is evident, due to the fact that the set consists of matrices, which are associative.
Since the set is also a representation of , we can express eq2 as:
^{\dagger}D^{-1/2}=D^{-1/2}\sum_{\gamma=1}^{\vert G\vert}\tilde A_{\gamma}\tilde A_{\gamma}^{\dagger}D^{-1/2}\\=D^{-1/2}DD^{-1/2}=D^{-1/2}D^{1/2}D^{1/2}D^{-1/2}=I)
Question
Explain why the 2nd equality in the above equation is valid.
Answer
^{\dagger}=\tilde A_{\alpha}(\tilde A_1+\tilde A_2+\cdots+\tilde A_{\vert G\vert})\[\tilde A_{\alpha}(\tilde A_1+\tilde A_2+\cdots+\tilde A_{\vert G\vert})\]^{\dagger}\\=(\tilde A_{\alpha}\tilde A_1+\tilde A_{\alpha}\tilde A_2+\cdots+\tilde A_{\alpha}\tilde A_{\vert G\vert})(\tilde A_{\alpha}\tilde A_1+\tilde A_{\alpha}\tilde A_2+\cdots+\tilde A_{\alpha}\tilde A_{\vert G\vert})^{\dagger})
According to the rearrangement theorem, each summand in 
is a unique element of , which is denoted by 
. Therefore, the 2nd equality in the equation before the Q&A holds.
Repeating the steps from eq2 for 
, we have 
. Therefore, is a unitary matrix.
Since , and 
, we have
^{-1}A_{\alpha}(UD^{1/2}))
In other words, every element of a representation of can undergo a similarity transformation that results in , which is unitary. This is necessary in proving Schur’s first lemma and Schur’s second lemma.