A symmetry element (not to be confused with a group element) is a point, a line, a plane or an axis with respect to which a symmetry operation is carried out. For three-dimensional objects, there are only 5 types of symmetry elements that need to be considered:

Question
Is a unique symmetry operation?
Answer
Yes, because an object with an symmetry element may not have a
symmetry element of the same
. For example, a tetragonal disphenoid has an
symmetry element but only a
symmetry element.
If an object has more than one symmetry axis of rotation, the one with the highest is called the principal axis, which is conventionally coincident with the -axis.
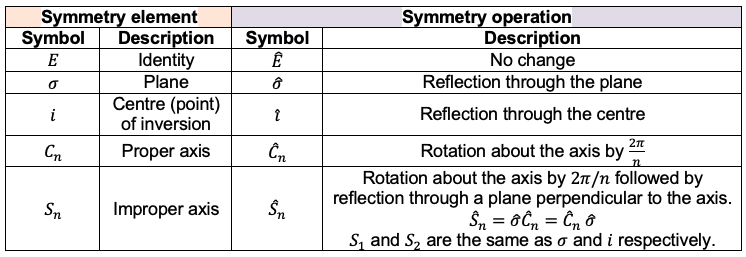
Consider an equilateral triangle in a three-dimensional real vector space (see figure I). It has a axis of symmetry and three planes of reflection. Figure II has a
axis of symmetry, while figure III has an
axis of symmetry and a centre of inversion
. All objects have the identity symmetry element.
A symmetry operation is a geometric transformation of an object with respect to a symmetry element in a real vector space such that the object looks the same after the transformation. However, the labelling of components of the object may be different post-transformation. For example, a reflection of the equilateral triangle in the -plane results in the triangle looking the same but the labels
and
being swapped.

Question
Why do we need to label the corners of the equilateral triangle?
Answer
Since the object is defined in a real vector space, each point on the object, and hence each label, is represented by a position vector. A symmetry operation preserves the magnitude of the position vector but changes its direction. For example, a reflection in the
-plane results in the triangle looking the same but transforms vector
to vector
(see diagram below). If we carry out two consecutive symmetry operations of
on the original triangle, vector
transforms into itself. This is equivalent to performing the symmetry operation
on the original triangle. Consequently, we are able to form mathematical groups, whose elements are symmetry operators, and use them to analyse the properties of objects like molecules.
In total, there are 6 symmetry elements and 6 associated symmetry operations for the equilateral triangle:


Question
What does the notation mean and why is the reflection in the
-plane not included in the set of symmetry operations for the equilateral triangle?
Answer
The angle of rotation is regarded as positive if the rotation is counter-clockwise when we look down the axis of rotation towards the origin (and hence the notation ).
and
can also be denoted as
and
respectively, where
is counter-clockwise by default and
is the double application of
. The reflection in the
-plane is a symmetry operation for the equilateral triangle but has the same effect as
and hence not included in the set.
If we conduct all 6 symmetry operations on the triangle, we find one ordered triple invariant: the origin. The significance of the invariant point and the two definitions above, together with the definition of a group, leads to an important mathematical group – the point group – which we’ll discussed in the next article.