The reduction of a two-particle problem to one-particle problems simplifies the Schrodinger equation by separating it into two one-particle equations. This process involves treating the two particles as if they were a single effective particle, utilising the concepts of center of mass and reduced mass .
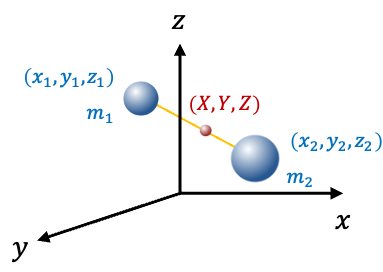
With reference to the above diagram, we define the relative coordinates of the system as
The coordinates of the center of mass of the two particles of masses
and
are

Question
How is centre of mass of the diatomic molecule derived?
Answer
The centre of mass can be derived via the principle of moments. For example, , which rearranges to
.
Substitute eq302 in eq303, we have
The magnitudes of the linear momentum vector of the particles with mass and
are
Substituting eq303a in eq304 and eq305 and summing the results, we have
where and
.

Question
Explain in detail the concept of reduced mass.
Answer
The reduced mass of two particles is a quantity that simplifies the description of the two-body problem, making it equivalent to a one-body problem, which consists of a fictitious particle of mass . Such a problem, e.g. one in the field of molecular vibrations, is easier to solve.
Eq306, which represents the total kinetic energy of the two particles, can be rewritten as
is expressed in center-of-mass coordinates and
is the total mass of the system. Therefore,
is the kinetic energy of the translational motion of the system, and consequently,
must describe the kinetic energy of the rotational motion and vibrational motion (collectively known as internal motion) of the system.
If the potential energy of the system is a function of the relative coordinates of the two particles, the Schrodinger equation is
Since translational motion is independent from rotational and vibrational motions, , where
and
are the translational energy of the system and the internal motion energy of the system respectively. This implies that
. Noting that translational energy is purely kinetic, we can separate eq307 into two one-particle problems:
Eq308 is a Schrodinger equation of a fictitious particle of mass that is subject to a zero-potential field, while eq309 is a Schrodinger equation of another fictitious particle of mass
that is under the influence of the potential
. Instead of relative cartesian coordinates
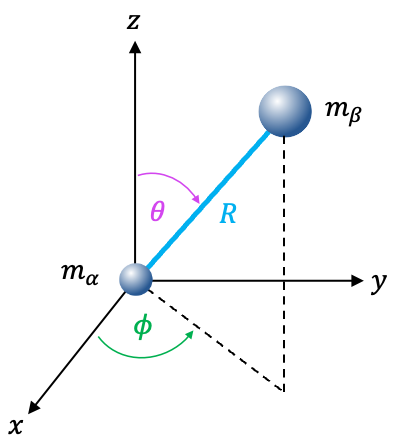
, the two equations can also be expressed in spherical coordinates
of one particle relative to the other (see diagram below):