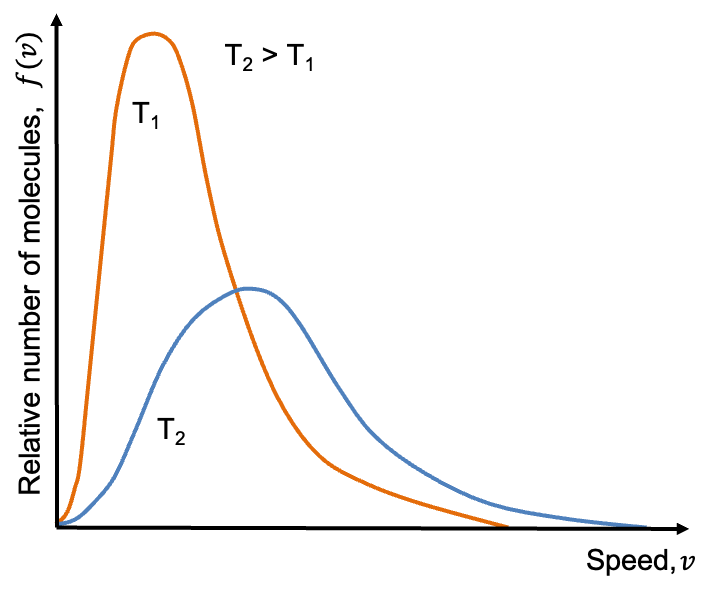
The Maxwell-Boltzmann distribution describes the range of speeds
among gaseous molecules of an ideal gas at a given temperature
.
The energy of an ideal gas molecule of mass is characterised solely by its kinetic energy
. For a molecule with velocity
, its energy is
, where
,
and
are the velocity vector components of
in Cartesian coordinates. Given that a molecule with the velocity magnitude
has the same energy regardless of direction, any molecule with the ordered triple
that lies on the surface of a sphere of radius
in velocity space belongs to the energy state
(see diagram below).

The fraction of molecules in the energy state is given by the Boltzmann distribution:
where
is the Boltzmann constant.
is the equilibrium temperature of the system.
is the number of molecules in the energy state.
is the total number of molecules in the system.
In probability theory, is the probability
of molecules in state
, with
being the normalisation constant. In other words,
, which we can rewrite as:
where is the probability density function (probability per unit interval of
) of molecules in a particular energy state
(we have dropped the index
for convenience) and
is the proportionality constant.
Since , where
,
As the probability density function is separable, its normalisation is equivalent to the separate normalisation of each of the individual functions:
Let’s evaluate just one of the integrals in eq4 by substituting in
to give

Question
Show that .
Answer
Let and at the same time let
since
and
are dummy variables.
In polar coordinates, . For infinitesimal changes, the change in area
can be approximated as a rectangle with sides
and
(see diagram below), with
.
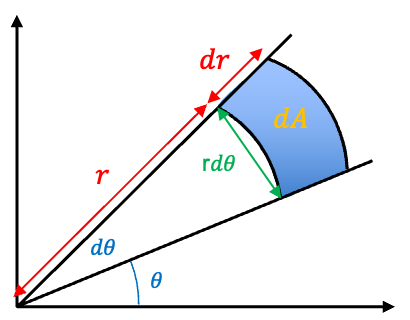
So,
Let
Hence, eq5 becomes,
Substituting eq6 in eq3,
Eq7 is known as the Maxwell-Boltzmann distribution for the velocity vector of a molecule. The fraction of molecules with velocity vectors in the infinitesimal range of
to
,
to
and
to
is
The fraction of molecules with speed in the infinitesimal range of
to
is then equivalent to the fraction of molecules with velocity vectors that lies within a spherical shell of infinitesimal thickness in velocity space (see diagram below).
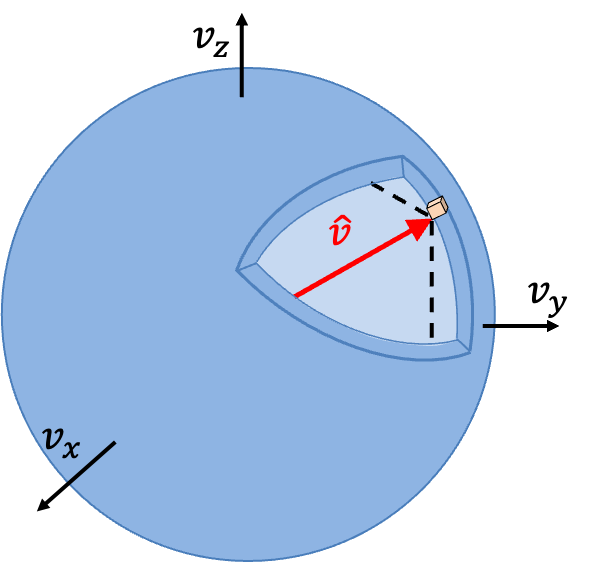
In other words,
where , and we have assumed that the volume of the shell of infinitesimal thickness is approximately equal to the sum of infinitesimal cubes, each with an infinitesimal volume of
.
Therefore, and
., which implies that the probability density function for the speed of a molecule
is
Eq9 is known as the Maxwell-Boltzmann distribution for the speed of a molecule. It also expresses the probability of a molecule being associated with a particular energy state. For a mole of an ideal gas, eq9 becomes
where is the mass of one mole of the gas and
is the gas constant.
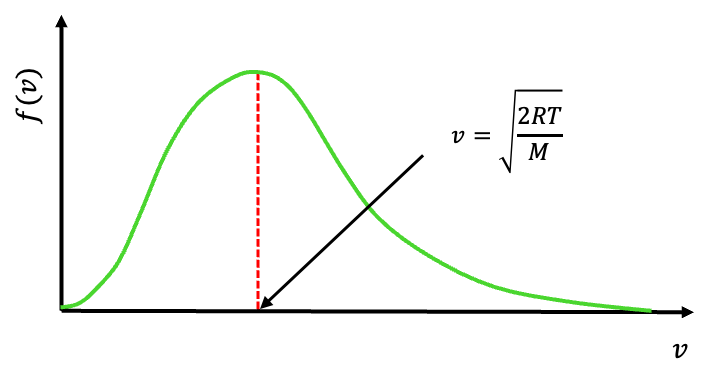

Question
Show that the most probable speed of one mole of an ideal gas is .
Answer
The most probable speed corresponds to the peak of the distribution (see above diagram). Carrying out the derivative , equating it to zero, and noting that the most probable speed
is neither
nor
, we have
.