Generating function for the Legendre Polynomials

The generating function for the Legendre polynomials is a mathematical tool that, when expanded as a power series, produces Legendre polynomials as its coefficients in terms of a variable.

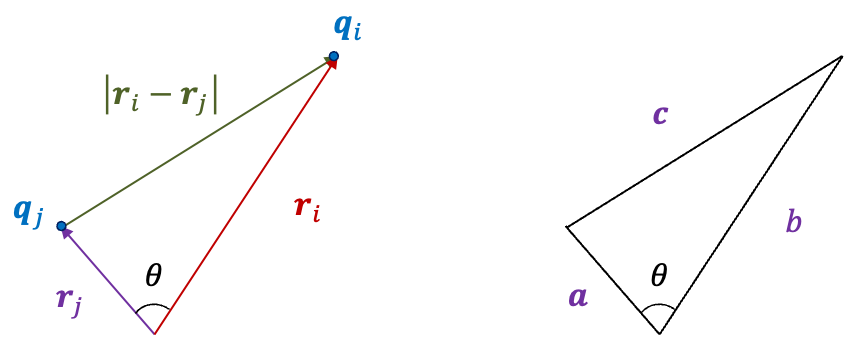
Legendre polynomials often arise in problems involving spherical harmonics. An example (see diagram above) is the multipole expansion $\frac{1}{\vert\boldsymbol{\mathit{r}}_i-\boldsymbol{\mathit{r}}_j\vert}=\frac{1}{r_i}\sum_{n=0}^{\infty}\biggr$\frac{r_j}{r_i}\biggr$^lP_l(cos\theta)$ . As the two points $q_i,q_j$ and the angle $\theta$ between them form a triangle, the Legendre polynomials $P_l(cos\theta)$ are related to the cosine rule $c=\sqrt{a^2+b^2-2abcos\theta}$ , which can be rearranged to

$\frac{b}{c}=\frac{1}{\sqrt{1-2tx+t^2}}\;\;\;\;\;\;\;\;343$

where $t=\frac{a}{b}$ and $x=cos\theta$ .

Since $\vert b\vert>\vert a\vert$ , we have $\vert t\vert<1$ and hence $\vert 2tx-t^2\vert<1$ . This implies that we can expand the RHS of eq343 as a binomial series:

$\frac{1}{\sqrt{1-2tx+t^2}}=\boldsymbol{1}+\boldsymbol{x}t+\biggr(\boldsymbol{\frac{3}{2}x^2-\frac{1}{2}}\biggr)t^2+\biggr(\boldsymbol{\frac{5}{2}x^3-\frac{3}{2}x}\biggr)t^3+\cdots\;\;\;\;\;\;\;\;344$