A rotation operator is a unitary operator that rotates quantum states by an angle
about an axis in a Hilbert space.
Mathematically, it is given by:
where , the angular momentum operator, is the generator of rotations about axis
.
To derive eq100, we begin by noting that the probability outcome of a quantum mechanical measurement is described by the Born interpretation:
where and
are wavefunctions representing quantum states.
Since rotations are symmetry operations that do not change physical probabilities, we require:
Using the matrix identity (see property 13 of this article for proof), we have
. Therefore,
is unitary, where
.
Let’s approximate as a power series of a small change in
:
where and
are first and second order rotation generator matrices respectively.
Since a rotation by zero angle must do nothing, , and eq101 (ignoring higher order terms) becomes
To preserve unitarity, . Expanding this equation and ignoring higher-order terms gives
or
. This implies that
is not Hermitian, which contradicts the postulate that all physical observables in quantum mechanics are represented by Hermitian operators. It follows that eq102 must have the following form:
For a quantum mechanical operator to represent the same physical observable in the passively rotated frame, its expectation value must be the same whether calculated in the initial frame or with respect to the new frame:
Substituting into eq104 gives
, which means that
and
are related by the similarity transformation
or equivalently,
where because
.
Substituting eq103 into eq105 yields:
where we have let the operator be the position operator .
Expanding eq106 and ignoring higher order terms results in , or equivalently,
where .
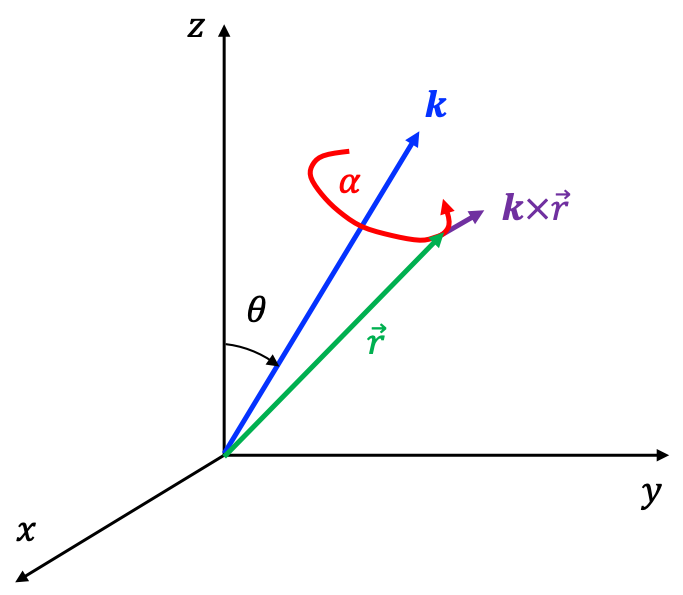
To determine the nature of , we refer to the active classical rotation of the vector
by an infinitesimal angle
about an arbitrary axis represented by the unit vector
(see diagram above), with the infinitesimal change in
given by:
where the cross product results in a vector with a magnitude proportional to and a direction tangential to the path of rotation.
Using the methodology of replacing classical variables with their quantum mechanical analogues to derive quantum mechanical expressions, eq108 becomes:
where we have added a minus sign because in eq108 is defined by an active rotation about the axis, while
in eq107 describes a passive rotation about the axis.

Question
Why is an active rotation and a passive rotation related by a negative sign in eq109?
Answer
An active rotation refers an anticlockwise rotation of a position vector in a fixed coordinate system by the angle (see this article for details). In a passive rotation, the position vector remains stationary while the coordinate system rotates around it. To produce the same effect on the coordinates, a passive rotation corresponds to an anticlockwise rotation of the coordinate system by
. In other words, a passive rotation of the coordinate system by
has the same result as an active rotation of the vector by
. Therefore,
.
Substituting into eq109 and expanding it gives:
Since ,
and
, we have:
Substituting into 107 and setting
to be the
-axis for simplicity gives:
Comparing eq110 with eq111 yields:
Comparing these three commutation relations with the total angular commutation relations of ,
and
, we find that
. In other words,
is the
-th component of the total angular momentum operator, expressed in units of
.
A finite rotation by an angle can be constructed by apply
successive infinitesimal rotations, each by an angle
. From eq103,

Question
Show that .
Answer
Let . So,
. Using the Taylor series
for small
, we have
As , we find that
, or equivalently,
. So,
. This makes eq112 the definition of the matrix exponential function.
Therefore, eq112 becomes:
Eq113 is usually written as:
where the eigenvalues of and hence
are expressed in units of
Since is a finite-dimensional linear operator acting on a finite-dimensional vector space,
can be represented by an
matrix in both group theory and quantum mechanical calculations. In general, the rotation operator in an Euler angle system, which is defined by three successive rotations by the angles
,
and
, is given by:
where ,
and
.
The application of eq115 involves the rotation operator transforming a quantum state with total angular momentum projection along the molecular axis into a linear combination of states
with the projection along the lab
-axis:
where , the entries of the Wigner D-matrix, are the coefficients of
.

Question
Why is the transformed state a linear combination of ?
If eq114 describes an operator that rotates quantum states by an angle about an axis
in a Hilbert space, how do three consecutive rotations described by eq115 ensure the complete transformation from the molecular coordinate system to the lab coordinate system?
Answer
In quantum mechanics, the states form a complete orthonormal basis in the Hilbert space corresponding to a fixed
. Therefore, any state with total angular momentum
, including the rotated state
, can be expressed as a linear combination of the basis states
.
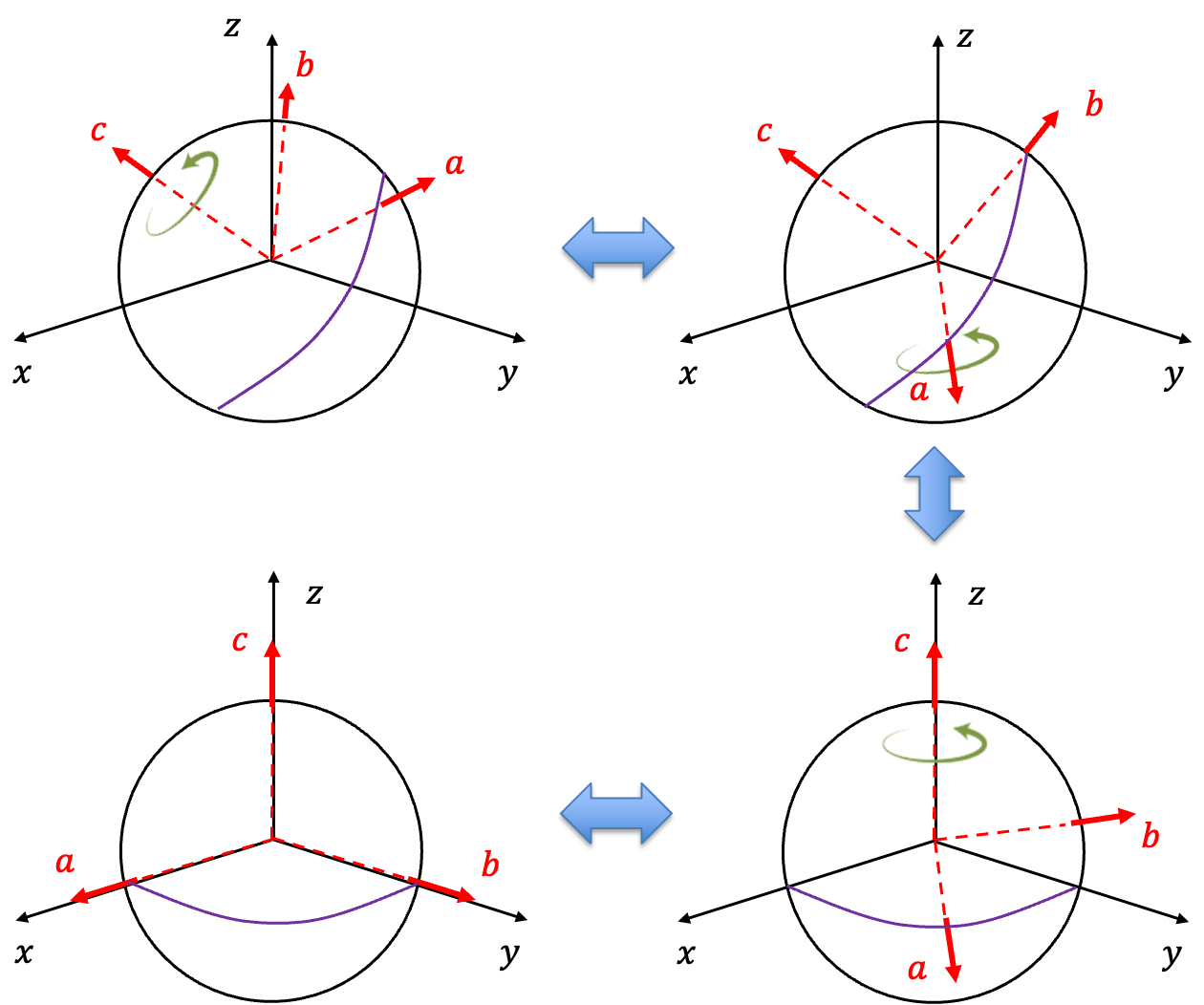
In the diagram above, represent the molecular axes, while
represent the lab-frame axes. Without assuming any specific rotation convention, the diagram illustrates that any target orientation can be achieved through three consecutive rotations. The first rotation about
brings
into the
-plane. The second rotation, about
, aligns
with
. Finally, the last rotation about
aligns the remaining axes of the two coordinate systems.