The energy-time uncertainty relation

The energy–time uncertainty relation states that the more precisely a system’s energy is defined, the longer it takes for the system to undergo a significant change.

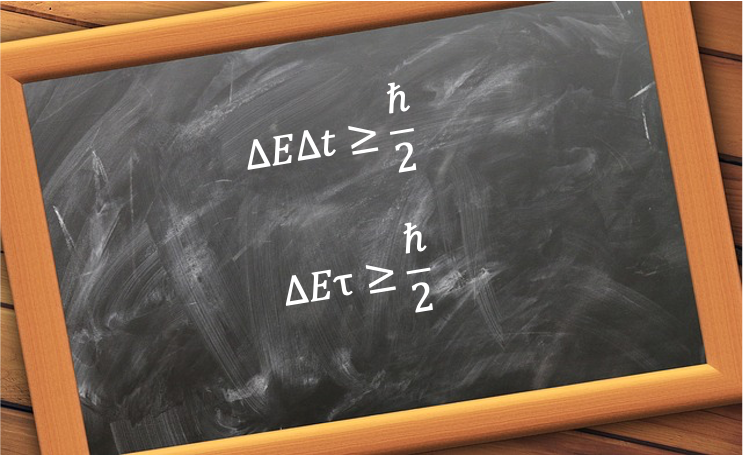
Mathematically, it is expressed as:

$\Delta E\Delta t\geq \frac{\hbar}{2}\; \; \; \; \; \; \; \; 27a$

It can be derived from the general form of the uncertainty principle $\Delta A\Delta B\geq \frac{1}{2}\vert\langle\psi\vert[\hat{A},\hat{B}]\vert\psi\rangle\vert$ , where $A$ and $B$ are the observables corresponding to the Hermitian operators $\hat{A}$ and $\hat{B}$ , respectively. In this case, we let $B$ be a system’s energy $E$ , which is the observable associated with the Hamiltonian operator $\hat{H}$ . Any uncertainty in $E$ therefore corresponds to a change in $\hat{H}$ .

However, in non-relativistic quantum mechanics, time $t$ is a parameter, not a Hermitian operator. Hence, we cannot replace $\hat{A}$ with a time operator $\hat{T}$ . Instead, we begin with the time evolution of the expectation value of an operator that does not explicitly depend on time:

$\langle\hat{A}\rangle=\langle\psi(t)\vert\hat{A}\vert\psi(t)\rangle\; \; \; \; \; \; \; \; 27b$

Question

What is an operator that does not explicitly depend on time?

Answer

An operator that does not explicitly depend on time is one whose definition does not contain time as a variable. For example, the angular momentum operator $\hat{L}_z=-i\hbar\frac{\partial}{\partial\phi}$ depends only on spatial coordinates and not on time. However, the state $\psi(t)$ on which the operator acts may evolve with time according to the Schrödinger equation. Therefore, even though the operator itself is time-independent, its expectation value can still change over time as the state evolves.

Differentiating eq27b with respect to time using the product rule gives:

$\frac{d}{dt}\langle\hat{A}\rangle=\biggr$\frac{d}{dt}\langle\psi(t)\vert\biggr$\hat{A}\vert\psi(t)\rangle+\langle\psi(t)\vert\hat{A}\biggr$\frac{d}{dt}\vert\psi(t)\rangle\biggr$\; \; \; \; \; \; \; \; 27c$

The time evolution of the state is governed by the time-dependent Schrödinger equation $\frac{d}{dt}\vert\psi(t)\rangle=-\frac{i}{\hbar}\hat{H}\vert\psi(t)\rangle$ . Taking its Hermitian conjugate yields $\frac{d}{dt}\langle\psi(t)\vert=\frac{i}{\hbar}\langle\psi(t)\vert\hat{H}$ . Substituting these two equations into eq27c results in:

$\begin{align}\frac{d}{dt}\langle\hat{A}\rangle&=\frac{i}{\hbar}\langle\psi(t)\vert\hat{H}\hat{A}\vert\psi(t)\rangle-\frac{i}{\hbar}\langle\psi(t)\vert\hat{A}\hat{H}\vert\psi(t)\rangle\\&=\frac{1}{i\hbar}\langle\psi(t)\vert\[\hat{A},\hat{H}\]\vert\psi(t)\rangle\; \; \; \; \; \; \; \; 27d\end{align}$

Question

Explain the Hermitian conjugate forms of $\frac{d}{dt}\vert\psi(t)\rangle$ and $-\frac{i}{\hbar}\hat{H}\vert\psi(t)\rangle$ .

Answer

Linear operators acting on the Hilbert space vectors can be represented by square matrices. The Hermitian conjugate (or complex transpose) of two such matrices is given by $(AB)^{\dagger}=B^{\dagger}A^{\dagger}$ (see property 13 of this article for proof). Therefore, $\biggr\[-\frac{i}{\hbar}\hat{H}\vert\psi(t)\rangle\biggr\]^{\dagger}=\frac{i}{\hbar}\langle\psi(t)\vert\hat{H}$ , where $i^{\dagger}=i^*=-i$ . However, $\frac{d}{dt}$ is a scalar operator acting on a scalar parameter. If $\vert\psi(t)\rangle=\sum_nc_n(t)\vert n\rangle$ , then

$\begin{align}\biggr\[\frac{d}{dt}\vert\psi(t)\rangle\biggr\]^{\dagger}&=\biggr\{\sum_n\biggr\[\frac{d}{dt}c_n(t)\biggr\]\vert n\rangle\biggr\}^{\dagger}\\&=\sum_n\biggr\[\frac{d}{dt}c^*_n(t)\langle n\vert\biggr\]\\&=\frac{d}{dt}\langle\psi(t)\vert\end{align}$

Comparing eq27d with the general uncertainty principle $\Delta A\Delta E\geq \frac{1}{2}\vert\langle\psi\vert[\hat{A},\hat{H}]\vert\psi\rangle\vert$ gives:

$\Delta A\Delta E\geq \frac{\hbar}{2}\biggr\vert\frac{d}{dt}\langle\hat{A}\rangle\biggr\vert\;\;\;\;\;\;\;\;27e$

where $\vert i\vert=\sqrt{0^2+1^2}=1$ .

Since $\biggr\vert\frac{d}{dt}\langle\hat{A}\rangle\biggr\vert=\frac{\Delta A}{\Delta t}$ , eq27e becomes the energy-time uncertainty relation. Here, $\Delta t$ corresponds to the time scale for the system’s evolution, i.e. the time required for the expectation value of $\hat{A}$ to change by one standard deviation $\Delta A$ .

An important example of this relation occurs in the excited state of a molecule, where $\Delta t$ corresponds to the lifetime $\tau$ of the excited state, and $\Delta E$ is the uncertainty in the transition energy between the excited and relaxed states. In other words, the shorter the lifetime of an unstable state, the larger the uncertainty in its transition energy. A large $\Delta E$ means the emitted photon’s energy is not a single, sharp value, but a range of values, leading to a broadened line in the spectrum.

The broadening of spectral lines can also be caused by molecular interactions. For example, collisions between atoms or molecules lead to shortened excited-state lifetimes by inducing transitions via a non-radiative pathway. When two particles approach closely enough to interact, their potential energy varies according to the internuclear distance, producing a perturbation that couples their internal energy levels. If part of the internal energy of particle A, which is in an excited state, is transferred to particle B during the collision, particle A undergoes collisional de-excitation, and the excess energy is converted into additional kinetic energy of the colliding pair rather than being emitted as a photon. This process effectively reduces the lifetime of the excited state, leading to spectral broadening.

Finally, since $\hbar=\frac{h}{2\pi}$ , eq27a is sometimes written less precisely as:

$\Delta E\tau\geq \hbar\;\;\;\;\;\;\;\;27f$

$\Delta E\tau\geq h\;\;\;\;\;\;\;\;27g$

The energy-time uncertainty relation

Question

Answer

Question

Answer

Next article: spectral decomposition of an operator

Previous article: The uncertainty principle (derivation)

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply