Determining the normal modes of CO2 using the descent of symmetry method

The descent of symmetry method offers an efficient approach to determining the normal modes of CO₂.

The conventional procedure for determining the normal modes of a molecule involves the following steps:

1. Forming a basis set of unit displacement vectors $B=(x_1,y_1,z_1,x_2,y_2,z_2,\cdots)$ representing the instantaneous motions of the atoms.
2. Determining geometrically the transformed vectors $B'=(x'_1,y'_1,z'_1,x'_2,y'_2,z'_2,\cdots)$ for each symmetry operation associated with the point group of the molecule.
3. Constructing the symmetry operation matrix $R$ such that $B'=RB$ .
4. Evaluating the trace of each matrix $R$ to obtain the character of the reducible representation, and decomposing each representation to determine the irreducible representations of the normal modes of the molecule.

However, CO₂ is a linear molecule belonging to the $D_{\infty h}$ point group, whose infinitely many symmetry elements render the above procedure impractical. The descent of symmetry method circumvents this difficulty by replacing $D_{\infty h}$ with a suitable finite subgroup, while preserving the essential symmetry properties of all $3N-9$ degrees of freedom. This is justified because

- the symmetry operations of both the parent group and its subgroup return the molecule to physically indistinguishable configurations; and
- both the parent group and its subgroup act on the same set of basis functions (e.g. the Cartesian displacement vectors), from which reducible representations of either group are generated and subsequently decomposed to obtain the irreducible representations of the respective group.

As a result, all the normal modes of a molecule that transform according to certain irreducible representations of a parent group must also transform according to irreducible representations of the subgroup. The final step is to match the irreducible representations of both groups through a process known as correlation.

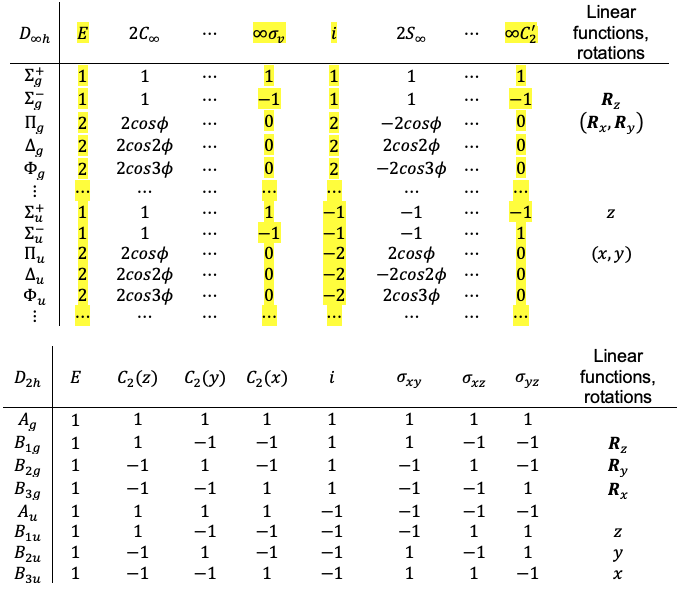
To proceed, we select an appropriate subgroup of $D_{\infty h}$ for constructing the transformation matrices. While not strictly required, it is generally advantageous for the chosen subgroup to contain symmetry elements belonging to the same classes as those of the parent group, in order to minimise ambiguity during the correlation step. A common and convenient choice is the $D_{2h}$ point group, which includes the key symmetry operations of $E$ , $C_{2}$ , $\sigma$ and $i$ preserved from the parent group.

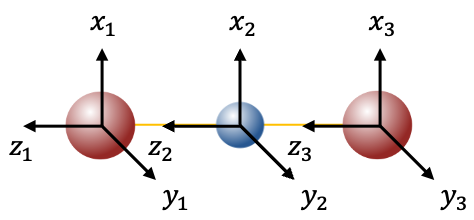
Next, we follow steps 1 to 3 by imposing the $D_{2h}$ symmetry operations on the set of nine unit displacement vectors $B=(x_1,y_1,z_1,x_2,y_2,z_2,x_3,y_3,z_3)$ . For example, the transformation matrix for inversion $i$ is:

$R_i=\begin{pmatrix}0&0&0&0&0&0&-1&0&0\\0&0&0&0&0&0&0&-1&0\\0&0&0&0&0&0&0&0&-1\\0&0&0&-1&0&0&0&0&0\\0&0&0&0&-1&0&0&0&0\\0&0&0&0&0&-1&0&0&0\\-1&0&0&0&0&0&0&0&0\\0&-1&0&0&0&0&0&0&0\\0&0&-1&0&0&0&0&0&0\end{pmatrix}$

where $B'=R_iB$ .

The eight transformation matrices form a reducible representation $\Gamma_{3N}$ of the $D_{2h}$ point group with the following traces:

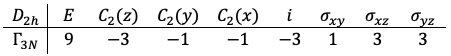
Using eq27a, $\Gamma_{3N}$ is decomposed to $\Gamma_{3N}=A_g\oplus B_{2g}\oplus B_{3g}\oplus 2B_{1u}\oplus 2B_{2u}\oplus 2B_{3u}$ . Subtracting the translational modes ( $B_{1u},B_{2u},B_{3u}$ ) and the rotational modes ( $B_{2g},B_{3g}$ ) gives the vibrational representation:

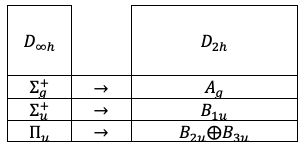
$\Gamma_{vib}=A_g\oplus B_{1u}\oplus B_{2u}\oplus B_{3u}$

The correlation step involves comparing the characters of symmetry operations common to both $D_{\infty h}$ and $D_{2h}$ , using their respective character tables. In particular:

- Since rotation about the $z$ -axis (intermolecular axis) is not a physical degree of freedom for a linear molecule, characters associated with $C_{2}(z)$ in $D_{2h}$ are not used in the correlation. Instead, the characters of $\infty C'_2$ in $D_{\infty h}$ are compared with those of $C_2(x)$ and $C_{2}(y)$ in $D_{2h}$ .
- Only the reflection planes $\sigma_{xz}$ and $\sigma_{yz}$ in $D_{2h}$ correspond to $\infty\sigma_v$ in $D_{\infty h}$ ( $\sigma_{xy}$ does not).

This leads to the following correlation between the irreducible representations of the two groups:

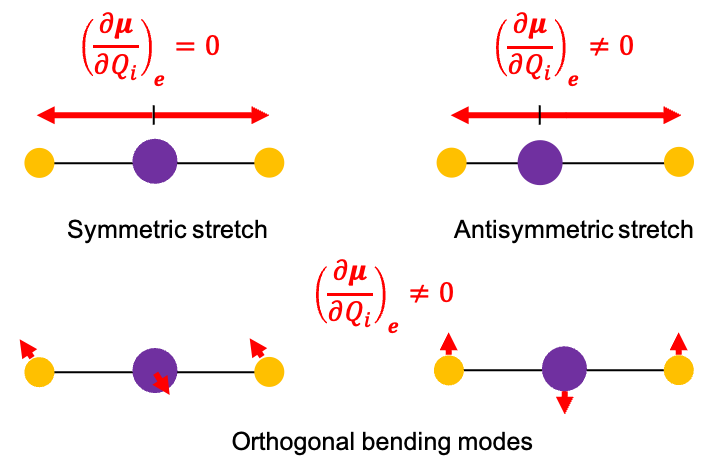
It is evident that the vibrational mode transforming according to the totally symmetric irreducible representation $A_g$ in $D_{2h}$ , and correspondingly according to $\Sigma^+_g$ (also totally symmetric) in $D_{\infty h}$ , represents the symmetric stretching motion of CO₂.

Two of the four vibrational modes are degenerate and transform according to $\Pi_u$ when the full $D_{\infty h}$ symmetry of CO₂ is considered. These two modes describe bending motions in mutually perpendicular planes and share the same vibrational frequency. Upon descending from $D_{\infty h}$ to $D_{2h}$ , this degeneracy is lifted, and the doubly degenerate bending mode splits into two symmetry-distinct components transforming as $B_{2u}$ and $B_{3u}$ .

The remaining vibrational mode transforms according to $\Sigma^+_u$ and is antisymmetric with respect to inversion, identifying it as the antisymmetric stretching mode.

Determining the normal modes of CO₂ using the descent of symmetry method

Question

Answer

Next article: Correlation diagram

Previous article: Subgroup (descent of symmetry)

Content page of group theory

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply