General selection rules for scattered radiation

Selection rules for scattered radiation describe the allowed changes in a molecule’s state during light scattering.

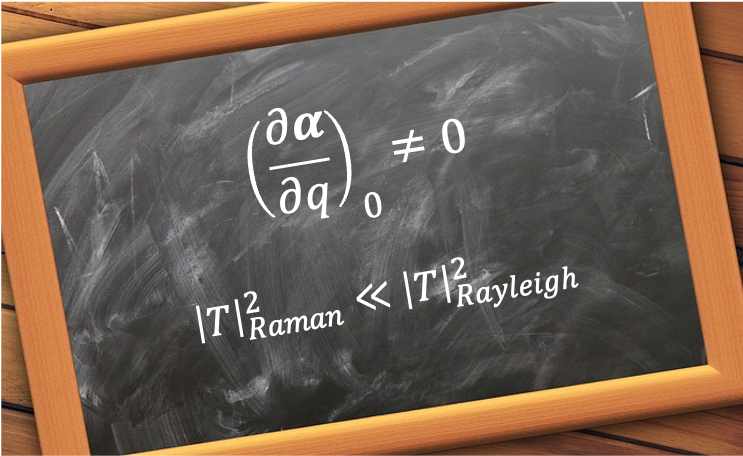
According to the time-dependent perturbation theory, the transition probability $\vert T\vert^2$ between the orthogonal states $\psi$ and $\psi'$ is proportional to the square of the corresponding transition matrix element $\vert\langle\psi'\vert\boldsymbol{\mathit{\hat{\mu}}}\vert\psi\rangle\vert^2$ . For example, in conventional rotational spectroscopy, this involves the electric dipole moment operator $\boldsymbol{\mathit{\hat{\mu}}}$ , and transitions occur only for molecules with a permanent dipole moment.

Transitions associated with scattering radiation, however, arise from an induced dipole moment rather than a permanent one. It follows, with reference to eq1, that the transition probability is given by:

$\vert T\vert^2=\vert\langle\psi'\vert\boldsymbol{\mathit{\hat{\mu}}}_{ind}\vert\psi\rangle\vert^2=E^2\vert\langle\psi'\vert\boldsymbol{\mathit{\alpha}}\vert\psi\rangle\vert^2$

Thus, a necessary condition for scattered-radiation transitions is that the matrix element $\boldsymbol{\mathit{E}}\vert\langle\psi'\vert\boldsymbol{\mathit{\alpha}}\vert\psi\rangle$ be non-zero. To examine this condition further, we consider how the molecular polarisability $\boldsymbol{\mathit{\alpha}}$ depends on the molecular coordinate $q$ , which may represent a rotational angle or a vibrational displacement. This dependence can be expressed through a Taylor series about the equilibrium configuration:

$\boldsymbol{\mathit{\alpha}}=\boldsymbol{\mathit{\alpha}}_0+\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0q+\cdots$

Substituting this series (and neglecting higher-order terms) into $T=\boldsymbol{\mathit{E}}\vert\langle\psi'\vert\boldsymbol{\mathit{\alpha}}\vert\psi\rangle$ gives:

$T=\boldsymbol{\mathit{E}}\biggr\[\boldsymbol{\mathit{\alpha}}_0\langle\psi'\vert\psi\rangle+\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0\langle\psi'\vert q\vert\psi\rangle\biggr\]$

Because the wavefunctions are orthogonal, the first term vanishes unless $\psi'=\psi$ , which corresponds to Rayleigh scattering. Consequently, a Raman transition can occur only if $\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0\neq 0$ , i.e. the polarisability of the molecule must change as it undergoes rotational or vibrational motion.

When $\psi'=\psi$ , we have $\vert T\vert^2=\vert T\vert^2_{Rayleigh}=\vert\boldsymbol{\mathit{E}}\vert^2\vert\boldsymbol{\mathit{\alpha}}_0\vert^2$ , which is the transition probability for Rayleigh scattering. When $\psi'\neq\psi$ , we have the transition probability for Raman scattering:

$\vert T\vert^2=\vert T\vert^2_{Raman}=\vert\boldsymbol{\mathit{E}}\vert^2\biggr\vert\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0\biggr\vert^2\vert\langle\psi'\vert q\vert\psi\rangle\vert^2$

Since $\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0$ represents a small perturbation of the electron cloud of the molecule, $\biggr\vert\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial q}\biggr$_0\biggr\vert^2\ll \vert\boldsymbol{\mathit{\alpha}}_0\vert^2$ . Furthermore, the magnitude of the transition matrix element $\langle\psi'\vert q\vert\psi\rangle$ is never large: for vibrational Raman scattering it is proportional to the small zero-point vibrational amplitude, while for rotational Raman scattering it is a dimensionless angular matrix element bounded by unity. Consequently,