Rotational Raman selection rules describe the allowed changes in a molecule’s rotational angular momentum states during inelastic light scattering.
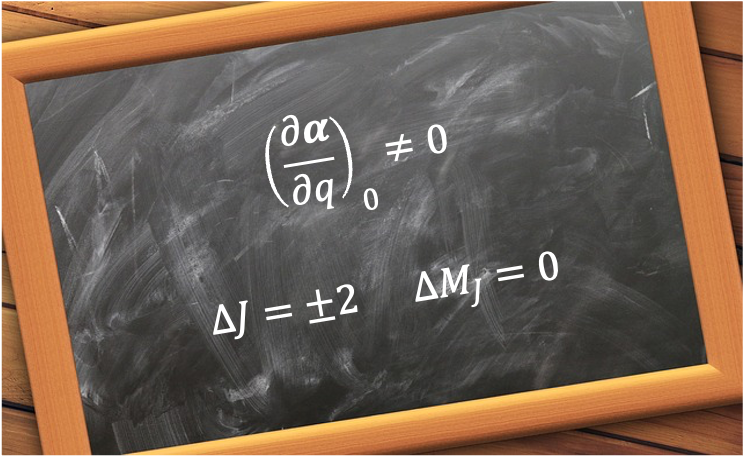
The explicit rotational Raman selection rules for a linear rotor can be derived by considering the molecule with a molecular frame interacting with an external electric field
applied along the laboratory
-axis (
).
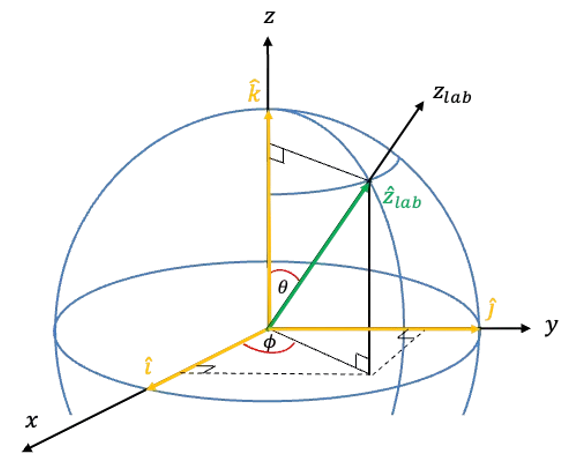
The angle is the polar angle between the molecular
-axis and the laboratory
-axis, while
is the azimuthal angle in the molecular
-plane, measured from the
-axis towards the
-axis (see diagram above).
The first step of the derivation involves expressing the induced dipole moment in terms of the molecular -axis before projecting it onto the direction of the electric field (laboratory
-axis).
Simple geometry shows that the direction cosines (the projections of the unit vector of the laboratory
-axis onto the molecular axes) are:
Similarly, the electric field applied along the laboratory -axis has the following components in the molecular frame:
In the molecular frame, the induced dipole moment is a vector with three components
:
where are the unit vectors along the molecular axes.
Likewise, the laboratory unit vector can be written in terms of the molecular frame as . Since the projection of any vector onto a unit vector is given by the dot product between the two vectors (see diagram below), the induced dipole moment
along the laboratory
-axis can be expressed by projecting
onto
as follows:

Substituting eq4 into eq6 yields:
For a linear molecule, the molecular axes coincide with the principal axes of the polarisability tensor, so that off-diagonal components vanish. Combining ,
and
with eq5 and eq7 results in:
Replacing and
with
, and
with
(since the molecular
-axis is the parallel axis of rotation, while the molecular
– and
-axes are the perpendicular axes of rotation), and using
, gives:
As explained in the previous article, the transition probability associated with scattered radiation is evaluated using , which in this case, is:
where and
are the un-normalised spherical harmonics.
The integral is equal to zero and
when
and
respectively. Thus, we require
for a probable transition to occur (
), resulting in:
where
is non-zero when either
or
is non-zero, or when both are non-zero. For the first integral, let
and
, giving:
which is non-zero only if , or equivalently,
This corresponds to Rayleigh scattering.
The second integral, with and
, is:
Substituting the recurrence relation into eq10 yields:
where
Letting in the same recurrence relation and substituting it into eq11 results in:
where
for a linear rotor because
.
and
are non-zero only if
, which gives the same Rayleigh scattering selection rule as eq9. For
to be non-zero, we require
or equivalently,
. The selection rule corresponding to
is
. Therefore, the selection rules for rotational Raman transition of a linear rotor are:

Question
Explain why is consistent with
for a linear rotor.
Answer
The polarisability of a linear rotor, as shown in the previous article, changes with the rotational angle
:
. This mirrors the fact that
. If
,the molecule is spherically symmetric and there is no change in
as the molecule rotates, i.e.
.
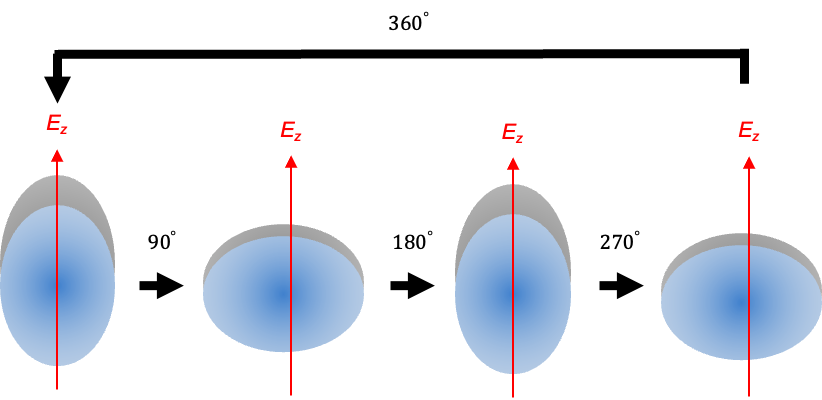
The selection rules can also be explained semiclassically, with the induced dipole moment given by:
where is the angular frequency of the incident radiation.
If the linear molecule is rotating an angular frequency , the value of its polarisability repeats twice per revolution cycle (see diagram above):
where is the constant baseline (average) polarisability of the molecule.
Substituting eq13 into eq12 gives:
Using the identity yields:
Eq14 shows that the induced dipole moment consists of three components: one oscillating at the incident frequency, and two at . Each time-dependent component of the induced dipole moment corresponds to an oscillating dipole, which radiates electromagnetic energy at the frequency at which it oscillates. It follows that the components oscillating at
and
give rise to Rayleigh-scattered radiation and Raman-scattered radiation respectively.

Question
Why does each component on the RHS of eq14 correspond to an oscillating, rather than the entire sum corresponding to a single oscillating dipole?
Answer
An oscillating electric dipole is defined by an electric dipole moment that varies sinusoidally in time at a single frequency, for example . Therefore, eq14 represents a superposition of three independent sinusoidal components, which can be viewed as a Fourier decomposition of the induced dipole moment. Each term oscillates at a distinct frequency and therefore corresponds to an independent oscillating dipole that radiates at that frequency.
Raman selection rules are often discussed for thermally populated rotational levels, where is typically large (the classical limit). For large
, the magnitude of the quantum angular momentum of the molecule is
. Substituting this approximation into
gives:
is the angular frequency of a Stokes-scattered photon, which is associated with the resultant quantum rotational transitional frequency of
. This corresponds to the selection rule
, because at large
,
Similarly, the angular frequency (anti-Stokes scattering) leads to the selection rule
.