Vibrational Raman selection rules

Vibrational Raman selection rules describe the allowed changes in a molecule’s vibrational states during inelastic light scattering.

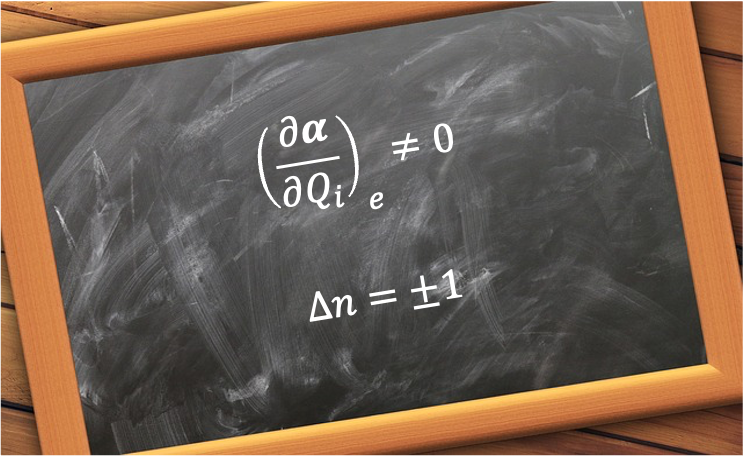
According to the time-dependent perturbation theory, the transition probability $\vert T\vert^2$ between the orthogonal vibrational states $\psi_k=N_kH_k\biggr$\sqrt{\frac{\omega_k}{\hbar}}Q_k\biggr$e^{-\frac{\omega_kQ^2_k}{2\hbar}}$ and $\psi_j=N_jH_j\biggr$\sqrt{\frac{\omega_j}{\hbar}}Q_j\biggr$e^{-\frac{\omega_jQ^2_j}{2\hbar}}$ is proportional to the square of the corresponding transition matrix element $\vert\langle\psi_j\vert\hat{\boldsymbol{\mathit{\mu}}}\vert\psi_k\rangle\vert^2$ . For example, in conventional infrared vibrational spectroscopy, this involves the electric dipole moment operator $\hat{\boldsymbol{\mathit{\mu}}}$ , and transitions occur only for molecules with a permanent dipole moment.

Transitions associated with scattering radiation, however, arise from an induced dipole moment rather than a permanent one. It follows, with reference to eq1, that the transition probability is given by:

$\vert T\vert^2=\vert\langle\psi_j\vert\hat{\boldsymbol{\mathit{\mu}}}_{ind}\vert\psi_k\rangle\vert^2=E^2\vert\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle\vert^2$

Thus, a necessary condition for scattered-radiation transitions is that the matrix element $\vert\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle\vert$ be non-zero. To examine this condition further, we consider how the molecular polarisability $\boldsymbol{\mathit{\alpha}}$ depends on the normal coordinate $Q_i$ for a molecule. This dependence can be expressed through a Taylor series about the equilibrium position:

$\boldsymbol{\mathit{\alpha}}=\boldsymbol{\mathit{\alpha}}_0+\sum_{i=1}^m\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_eQ_i+\cdots\;\;\;\;\;\;\;\;40$

For the sole excitation of a single normal mode $i$ , we multiply eq40 on the left and right by $\psi_J=\vert n_a,n_b,\cdots,n_i^{'},\cdots,n_m\rangle$ and $\psi_k=\vert n_a,n_b,\cdots,n_i,\cdots,n_m\rangle$ respectively and integrate over all space to give,

$\begin{align}\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle&=\boldsymbol{\mathit{\alpha}}_0\langle\psi_j\vert\psi_k\rangle+\sum_{i=1}^m\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\langle\psi_j\vert Q_i\vert\psi_k\rangle\\&=\boldsymbol{\mathit{\alpha}}_0\langle\psi_j\vert\psi_k\rangle+\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\langle\psi_j\vert Q_i\vert\psi_k\rangle\;\;\;\;\;\;\;\;41\end{align}$

where the second equality is due to the fact that $\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e=0$ for all the other non-excited normal modes, which remain at their equilibrium positions.

Because the wavefunctions are orthogonal, the first term vanishes unless $\psi_j=\psi_k$ , which corresponds to Rayleigh scattering. Consequently, a Raman transition can occur only if $\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\neq 0$ , i.e. the polarisability of the molecule must change as it undergoes vibrational motion.

Setting $\psi_j\neq\psi_k$ and expanding eq41 yields:

$\begin{align}\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle&=\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\int\cdots\int\psi^*_{n_a}\psi^*_{n_b}\cdots\psi^*_{n_i^{'}}\cdots\psi^*_{n_m}Q_i\psi_{n_a}\psi_{n_b}\cdots\psi_{n_i},\cdots\psi_{n_m}dQ_a\cdots dQ_m\\&=\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\int\psi^*_{n_i^{'}}Q_i\psi_{n_i}dQ_i\;\;\;\;\;\;\;\;42\end{align}$

Substituting the recurrence relation eq32ab in eq42 gives:

$\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle\propto\biggr$\frac{\partial\boldsymbol{\mathit{\alpha}}}{\partial Q_i}\biggr$_e\biggr\[\sqrt{\frac{\hbar(n_i+1)}{2\omega}}\delta_{n_i^{'}n_i+1}+\sqrt{\frac{\hbar n_i}{2\omega}}\delta_{n_i^{'}n_i-1}\biggr\]$

For $\langle\psi_j\vert\boldsymbol{\mathit{\alpha}}\vert\psi_k\rangle$ to be non-zero, $n_i^{'}=n_i+1$ or $n_i^{'}=n_i-1$ . Therefore, the vibrational Raman selection rules are