Good quantum state

A good quantum state is an eigenstate of the system Hamiltonian whose associated quantum numbers are conserved and uniquely label the state.

Such states arise from the symmetries of the Hamiltonian. As eigenstates of the Hamiltonian, they are unchanged under time evolution apart from an overall phase and provide a stable basis for describing physical observables and selection rules by enabling the diagonalisation of the Hamiltonian.

For example, a hydrogen atom is described by the good quantum state $\vert n,l,m_l,m_s\rangle$ if spin-orbit coupling is ignored. The principal quantum number $n$ counts the number of radial nodes in the electron wavefunction, which is fixed for a given energy level. Therefore, $n$ remains conserved, and energy shells labeled by $n$ are always well-defined, making it a good quantum number. The remaining quantum numbers are also good quantum numbers because their corresponding operators commute with the Hamiltonian $\hat{H}$ . We refer to $\vert n,l,m_l,m_s\rangle$ as an uncoupled basis state.

Question

Show that $\hat{L}^2$ , $\hat{l}_z$ and $\hat{S}_z$ commute with the Hamiltonian.

Answer

For $\hat{L}^2$ and $\hat{l}_z$ , see the Q&A in this article by replacing $\hat{J}^2$ and $\hat{J}_z$ with $\hat{L}^2$ and $\hat{l}_z$ .

The non-relativistic Hamiltonian $\hat{H}=\frac{p^2}{2m}+V(r)$ involves only spatial coordinates. Since $\hat{S}_z$ acts on a different Hilbert space (spin coordinate $\sigma$ ), it always commutes with $\hat{H}$ :

$\hat{H}\hat{S}_z\psi(r)\chi(\sigma)=\hat{H}\psi(r)\hat{S}_z\chi(\sigma)=\hat{S}_z\chi(\sigma)\hat{H}\psi(r)=\hat{S}_x\hat{H}\psi(r)\chi(\sigma)$

However, when spin-orbit coupling is included, the Hamiltonian is given by $\hat{H}=\hat{H}_0+\hat{H}_{so}$ , where $\hat{H}_0$ is the non-relativistic Hamiltonian and $\hat{H}_{so}\propto\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}$ is the perturbation due to spin-orbit coupling. In this case, $m_l$ and $m_s$ are no longer good quantum numbers, and the system is described by the good quantum state $\vert n,l,j,m_j\rangle$ , known as the coupled basis state. $n$ and $l$ remain good because $\hat{H}_{so}$ is a weak perturbation that does not significantly mix energy states labelled by these quantum numbers.

Question

What is a mixing of energy states?

Answer

“Mixing” means that energy states are perturbed. These new energy levels can no longer be described by a stationary-state like $\vert n,l,m_l,m_s\rangle$ , but instead by a linear combination, e.g.:

$\vert\psi_{new}\rangle=\vert n,l,m_l,m_s\rangle+\vert n,l,m_l',m_s'\rangle$

This new state does not have a single value for $m_l$ or $m_s$ , making them “bad” quantum numbers.

As mentioned eariler, $\hat{J}^2$ commutes with $\hat{H}_0$ . It also commutes with $\hat{H}_{so}$ because

$\hat{J}^2=(\hat{\boldsymbol{\mathit{L}}}+\hat{\boldsymbol{\mathit{S}}})^2=\hat{L}^2+\hat{S}^2+2\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}$

So, $\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}=\frac{1}{2}(\hat{J}^2-\hat{L}^2-\hat{S}^2)$ and $[\hat{H}_{so},\hat{J}^2]$ is proportional to

$[\hat{J}^2-\hat{L}^2-\hat{S}^2,\hat{J}^2]=[\hat{J}^2,\hat{J}^2]-[\hat{L}^2,\hat{J}^2]-[\hat{S}^2,\hat{J}^2]=0$

Question

Why is $[\hat{J}^2,\hat{J}^2]-[\hat{L}^2,\hat{J}^2]-[\hat{S}^2,\hat{J}^2]=0$ ?

Answer

Since any operator commutes with itself, $[\hat{J}^2,\hat{J}^2]=0$ . For the 2^nd term,

$[\hat{L}^2,\hat{J}^2]=[\hat{L}^2,\hat{L}^2]+[\hat{L}^2,\hat{S}^2]+[\hat{L}^2,\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}]=[\hat{L}^2,\hat{S}^2]+[\hat{L}^2,\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}]$

$\hat{L}^2$ and $\hat{S}^2$ commute because they act on different Hilbert spaces (space vs spin). Expanding $[\hat{L}^2,\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}]$ gives:

$[\hat{L}^2,\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}]=[\hat{L}^2,\hat{L}_x\hat{S}_x]+[\hat{L}^2,\hat{L}_y\hat{S}_y]+[\hat{L}^2,\hat{L}_z\hat{S}_z]$

Using the identity $[\hat{A},\hat{B}\hat{C}]=[\hat{A},\hat{B}]\hat{C}+\hat{B}[\hat{A},\hat{C}]$ , we find that $[\hat{L}^2,\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}]=0$ . Substituting $\hat{J}^2=\hat{L}^2+\hat{S}^2+2\hat{\boldsymbol{\mathit{L}}}\cdot\hat{\boldsymbol{\mathit{S}}}$ into the 3^rd term and applying the same logic yields $[\hat{S}^2,\hat{J}^2]=0$ .

Since $\hat{J}^2$ commutes with both $\hat{H}_0$ and $\hat{H}_{so}$ , we have $[\hat{H}_0+\hat{H}_{so},\hat{J}^2]=0$ , with $j$ being a good quantum number. It follows that $m_j$ is a good quantum number because $[\hat{H}_0+\hat{H}_{so},\hat{J}_z]=0$ .

In the presence of an external magnetic field, the classification of a quantum number as “good” or “bad” depends on which interaction dominates the physical behaviour of the system. The Hamiltonian for the hydrogen atom becomes:

$\hat{H}=\hat{H}_0+\hat{H}_{so}+\hat{H}_Z$

where $\hat{H}_Z$ is the pertubration due to the Zeeman effect.

In a weak magnetic field, where $\hat{H}_Z\ll\hat{H}_{so}$ , the spin-orbit interaction is the dominant perturbation and $\vert n,l,j,m_j\rangle$ remains a good quantum state. The weak Zeeman field slightly shifts these states but is too weak to significantly mix states of different $j$ . In this sense, $j$ may be regarded as a “mostly good” quantum number, allowing the energies to be calculated accurately using perturbation theory.

In a strong external magnetic field $\hat{H}_Z\gg\hat{H}_{so}$ , torques are generated separately on the orbital and spin magnetic moments, $\boldsymbol{\mathit{\mu}}_l$ and $\boldsymbol{\mathit{\mu}}_s$ , with the vectors $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ antiparallel to $\boldsymbol{\mathit{\mu}}_l$ and $\boldsymbol{\mathit{\mu}}_s$ respectively. Each torque, $\boldsymbol{\mathit{\tau}}=\frac{d\boldsymbol{\mathit{L}}}{dt}$ or $\boldsymbol{\mathit{\tau}}=\frac{d\boldsymbol{\mathit{S}}}{dt}$ , is perpendicular to the external magnetic field direction (taken as the lab $z$ -axis), so its component along the field axis is zero. Consequently, the projections $l_z$ and $s_z$ cannot change. The only way for $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ to evolve in time while maintaining constant projections onto the $z$ -axis is for them to precess independently about the direction of the magnetic field. Hence, $m_l$ and $m_s$ become good quantum numbers again, and the state returns to the uncoupled form $\vert n,l,m_l,m_s\rangle$ .

Question

Does any precession occur in the hydrogen atom in the absence of an external magnetic field?

Answer

Yes, it does. In the rest frame of the electron, the positively charged nucleus orbits the electron. Since a moving charge creates a magnetic field, an internal magnetic field $\boldsymbol{\mathit{B}}_{so}$ parallel to $\boldsymbol{\mathit{L}}$ is produced from the electron’s perspective by its own orbital motion. $\boldsymbol{\mathit{B}}_{so}$ interacts with the electron’s spin magnetic moment $\boldsymbol{\mathit{\mu}}_s$ , generating a torque:

$\boldsymbol{\mathit{\tau}}=\boldsymbol{\mathit{\mu}}_s\times\boldsymbol{\mathit{B}}_{so}\propto\boldsymbol{\mathit{S}}\times\boldsymbol{\mathit{L}}$

Mathematically, this requires $\boldsymbol{\mathit{S}}$ to precess about $\boldsymbol{\mathit{L}}$ . However, if $\boldsymbol{\mathit{L}}$ were constant while $\boldsymbol{\mathit{S}}$ precessed around it, the total angular momentum $\boldsymbol{\mathit{J}}=\boldsymbol{\mathit{L}}+\boldsymbol{\mathit{S}}$ would change. However, in an isolated atom, $\boldsymbol{\mathit{J}}$ must be conserved. To ensure this, an equal and opposite torque acts on $\boldsymbol{\mathit{L}}$ as the internal interaction pulls on $\boldsymbol{\mathit{S}}$ , causing both $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ to evolve in time. 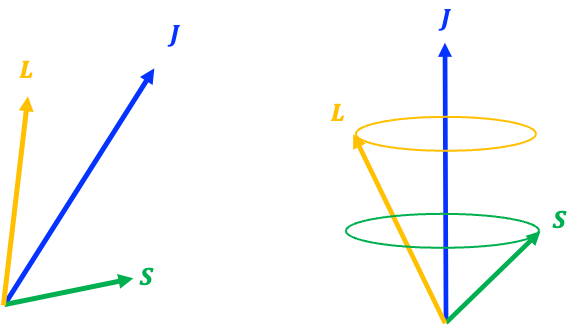The only way for both $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ to change while keeping $\boldsymbol{\mathit{J}}$ constant is for them to precess about their vector sum $\boldsymbol{\mathit{J}}$ (see diagram above).

In the presence of a strong external magnetic field $\boldsymbol{\mathit{B}}_Z$ , the precessional motion due to the interaction of $\boldsymbol{\mathit{B}}_Z$ with $\boldsymbol{\mathit{\mu}}_J$ becomes dominant, overwhelming the mutual precession of $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ around $\boldsymbol{\mathit{J}}$ . This leads to the decoupling of $\boldsymbol{\mathit{L}}$ and $\boldsymbol{\mathit{S}}$ .

Good quantum state

Question

Answer

Question

Answer

Question

Answer

Question

Answer

Previous article: Good quantum number

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply