The Rodrigues’ formula for the Legendre polynomials is a mathematical expression that provides a method to calculate any Legendre polynomial using differentiation.
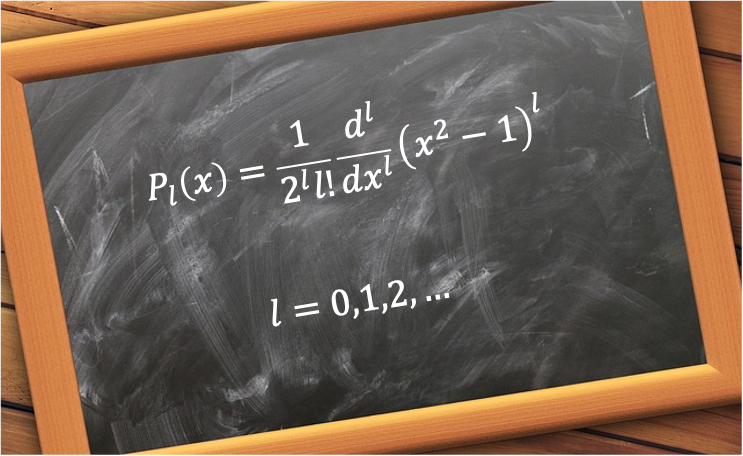
It is given by
with the first few Legendre polynomials being .
To derive eq348, let . The derivative of
with respect to
is
or equivalently,
Using Leibniz’s theorem to differentiate eq349 by times with respect to
gives
Comparing eq350 with eq332 reveals that is a solution to the Legendre differential equation. However, this solution does not produce the conventional Legendre polynomials of
and so on.

Question
Prove by induction that for
, and hence,
.
Answer
For , we have
. Assuming that
is true, then,
So, holds for all
. Similarly,
. If we let
, then
.
To derive the factor in eq348, we again use Leibniz’s theorem to find the
-th derivative of
with respect to
:
If we evaluate at
, only the
term in
survives because the binomial theorem defines
, resulting in
Since the conventional Legendre polynomials are defined by the condition , the solution to the Legendre differential equation in terms of
must be
, which is equivalent to eq348.