The generating function for the associated Laguerre polynomials is a mathematical tool that, when expanded as a power series, produces associated Laguerre polynomials as its coefficients in terms of a variable.
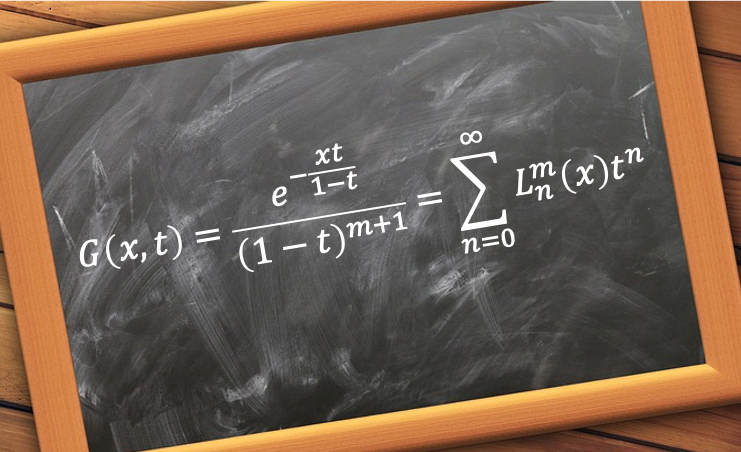
It is defined as
To prove eq448, we differentiate the generating function for the Laguerre polynomials (see eq430) times with respect to
to give
When , the terms in the summation equal zero. So,
From eq443, , which when substituted in the above equation yields,
Letting gives
which rearranges to eq448.