The associated Laguerre polynomials are a sequence of polynomials that are solutions to the associated Laguerre differential equation:
}{dx^2}+(m+1-x)\frac{dL_n^m(x)}{dx}+nL_n^m(x)=0\;\;\;\;\;\;\;442)
where =\frac{d^m}{dx^m}L_{n+m}(x))
are the associated Laguerre polynomials.
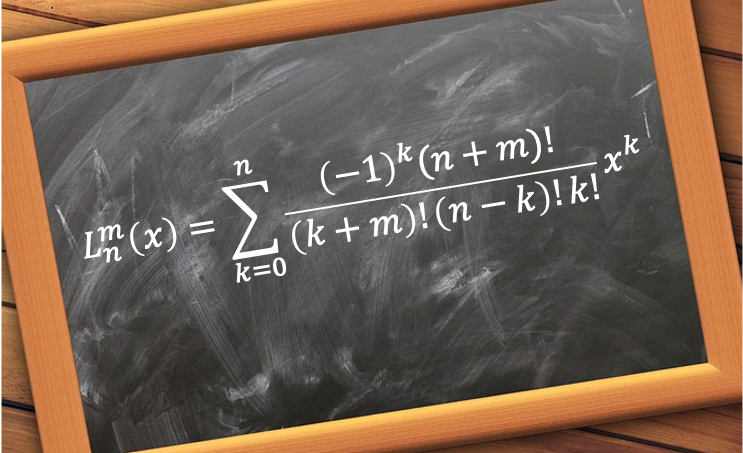
To show that 
are solutions to eq442, we refer to eq420, where \frac{dL_n}{dx}+nL_n=0)
. Letting 
, we have \frac{dL_{n+m}}{dx}+(n+m)L_{n+m}=0)
. Differentiating this equation 
times with respect to 
gives
+\frac{d^m}{dx^m}\biggr\[(1-x)\frac{dL_{n+m}}{dx}\biggr\]+(n+m)\frac{d^mL_{n+m}}{dx^m}=0)
Applying Leibniz’ theorem,
}{dx^k}\frac{d^{m-k+1}L_{n+m}}{dx^{m-k+1}}+(n+m)\frac{d^mL_{n+m}}{dx^m}=0)
\frac{d^{m+1}L_{n+m}}{dx^{m+1}}-m\frac{d^{m}L_{n+m}}{dx^{m}}+(n+m)\frac{d^{m}L_{n+m}}{dx^{m}}=0)
\frac{d^{m+1}L_{n+m}}{dx^{m+1}}+n\frac{d^{m}L_{n+m}}{dx^{m}}=0)
This implies that . Since ^m\frac{d^m}{dx^m}L_{n+m}(x))
is also a solution to the associated Laguerre differential equation, )
can also be expressed as
=(-1)^m\frac{d^m}{dx^m}L_{n+m}(x)\;\;\;\;\;\;\;\;443)
When 
, eq442 becomes the Laguerre differential equation. Therefore, =L_n(x))
. Substituting eq425 in eq443 yields
=(-1)^m\frac{d^m}{dx^m}\sum_{j=0}^{n+m}(-1)^j\frac{(n+m)!}{(j!)^2(n+m-j)!}x^j)
For 
, the terms in the summation equal zero. For 
, we note that \cdots (j-m+1)x^{j-m}=\frac{j!}{(j-m)!}x^{j-m})
, and so,
=(-1)^m\sum_{j=m}^{n+m}(-1)^j\frac{(n+m)!}{j!(n+m-j)!(j-m)!}x^{j-m})
Letting 
,
=\sum_{k=0}^{n}(-1)^k\frac{(n+m)!}{(k+m)!(n-k)!k!}x^{k}\;\;\;\;\;\;\;\;444)
Eq444 is the general expression for the un-normalised associated Laguerre polynomials. Using eq444, the first few associated Laguerre polynomials in terms of are
=1)
=1+m-x)
=\frac{1}{2}[x^2-2(m+2)x+(m+1)(m+2)])