pH, which stands for power of hydrogen, is a measure of the acidity of an aqueous solution. It is defined as:
where [H+] is the concentration of the aqueous hydrogen ion.
The concept was developed by the Danish chemist, Soren Peder Lauritz Sorensen in 1909.
Question
Why is pH defined on a logarithmic scale and why does it have a negative sign in front?
Answer
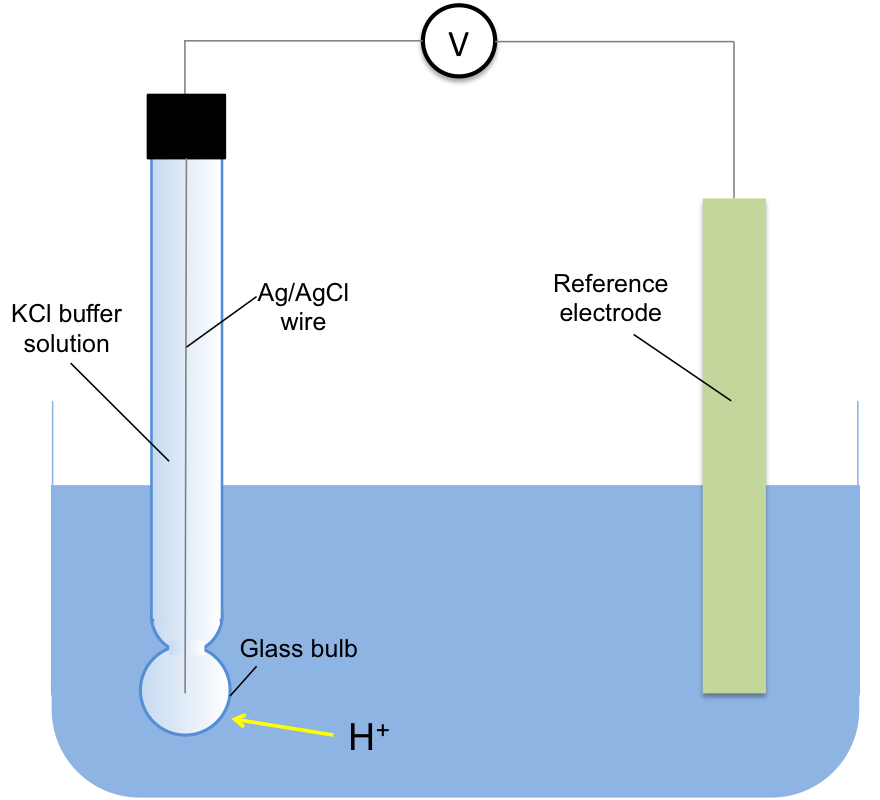
The most accurate way of measuring the concentration of H+ in a solution is using a glass electrode, a type of ion-selective electrode (see below diagram). The voltage, E, of the electrochemical cell containing the electrode is measured at 25oC and the concentration of H+ is determined by the Nernst equation:
Scientists found that the values generated by the factor log[H+] at different voltages are accurate over the range of -14 to 0 and decided to use it to conveniently express the concentration of H+ in a solution. As it is easier to deal with positive numbers (i.e. 0 to 14 instead of -14 to 0), pH is defined as –log[H+], which makes eq2:
