The first law of thermodynamics states that the change in internal energy of a system is the sum of the energy transferred to the system, due to a difference in temperature between the system and its surroundings, and the work done on the system by the surroundings.
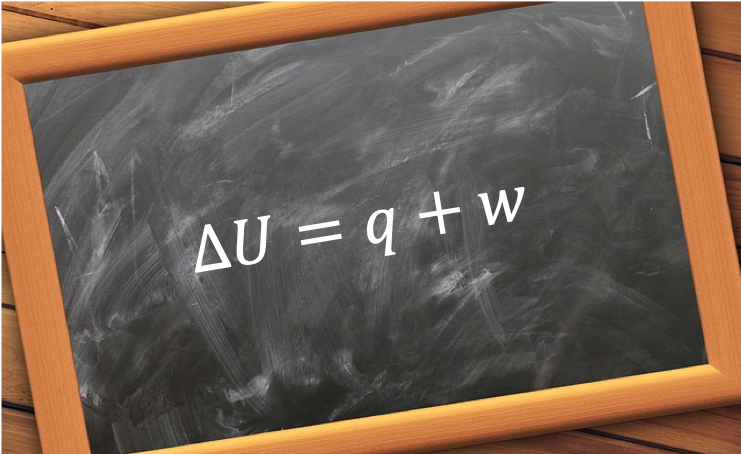
The internal energy of a system is defined as the sum of all the energies of molecules in the system. These energies include:
- Relativistic rest mass energies of electrons and nuclei (i.e. energies attributed to the existence of the molecules)
- Intramolecular translational, rotational, vibrational and electronic energies
- Intermolecular forces of interaction
is a thermodynamic property of a system. However, judging from the composition of
, it is very difficult to measure
directly. An alternate representation of
therefore needs to be established to characterise the internal energy of a system.
According to the theory of conservation of energy, energy can neither be created nor destroyed but can be transformed from one form to another. Energy can also be transferred between thermodynamic systems or from a system to its surroundings.
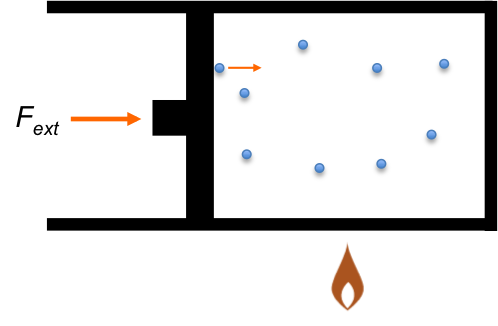
Consider a closed piston-cylinder system containing a gas (see diagram above). The internal energy of the system increases when thermal energy flows into it, or when a force is applied on the piston, compressing the gas. By the theory of conservation of energy,
where
is the change in internal energy of the system
(or heat) is the transfer of energy to the system due to a difference in temperature
(or work) is work done on the system by the surroundings (transfer of energy to the system not due to a difference in temperature)
Eq24 is known as the first law of thermodynamics. Instead of considering the absolute internal energy of a system when we study processes, we analyse the change in internal energy of the system, which is easily quantified by accounting for the amount of energy transferred to and from the system in the form of and
(refer to the next article for quantification of
). From an earlier article, reversible work done on the system is given by
. Therefore, for a system undergoing a reversible PV process, eq24 becomes
If the walls of the cylinder and piston are adiabatic, the system is isolated and . Eq24 becomes
which states that work done on an isolated system is exactly equal to the increase in the internal energy of the system.

Question
Describe the work-energy theorem and show that it is consistent with eq26 for work done on a monoatomic ideal gas in an adiabatic piston-cylinder system.
Answer
The work-energy theorem states that the net work done on a particle is equal to the change in the kinetic energy of the particle. This can be shown as follows:
Since the internal energy of a monoatomic ideal gas is entirely in the form of the kinetic energy of the gas, the work done on the gas in an adiabatic system is equal to the change in the internal energy of the gas.
Suppose the piston is now rendered immovable and the walls of the cylinder are thermally conducting, we have a closed constant volume system. Eq25 becomes
The change in internal energy of the system at constant volume can then be experimentally determined by quantifying the heat transferred to the system.