One-particle, time-dependent Schrodinger equation

The one-particle, time-dependent Schrodinger equation is a partial differential equation whose solutions are the one-particle, time-dependent wave functions of quantum-mechanical systems.

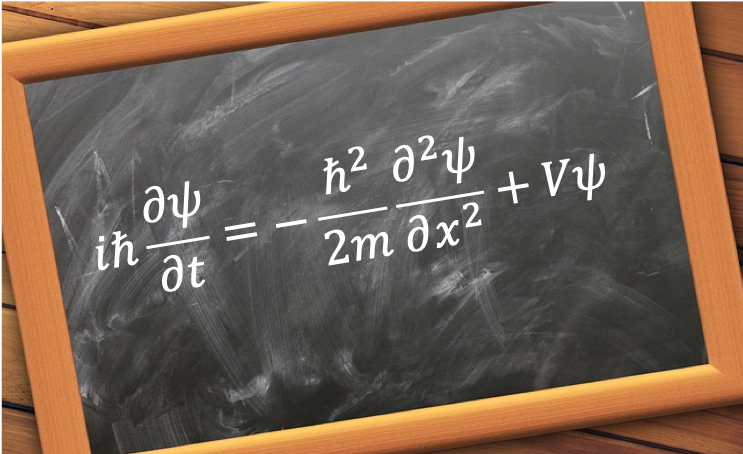
Even though the equation is widely regarded as a postulate, we can derive it using a general travelling wave equation $\psi(x,t)=Acos\frac{2\pi}{\lambda}(x-ct)$ . Since cosine is an even function, $Acos\frac{2\pi}{\lambda}(x-ct)=Acos\frac{2\pi}{\lambda}(ct-x)$ , which in the complex square-integrable form is: $\psi(x,t)=Ae^{-i\frac{2\pi}{\lambda}(ct-x)}$ . Since $c=v\lambda$ , we have $\psi(x,t)=Ae^{-i2\pi( vt-\frac{x}{\lambda} )}$ . Substituting Planck’s relation and de Broglie’s hypothesis in the wave equation, which is a mathematical description of the properties of a quantum-mechanical particle, we have $\psi(x,t)=Ae^{-\frac{i}{\hbar}(Et-xp )}$ , where $\hbar=\frac{h}{2\pi}$ .

The total energy of the particle is: $E=T+V=\frac{p^{2}}{2m}+V$ , and so

$E\psi=\frac{p^{2}\psi}{2m}+V\psi\; \; \; \; \; \; \; \; 54$

To develop an expression for $E\psi$ , we find the partial derivative of $\psi$ with respect to $t$ :

$\frac{\partial}{\partial t}Ae^{-\frac{i}{\hbar}(Et-xp)}=Ae^{\frac{i}{\hbar}xp}\frac{\partial}{\partial t}e^{-\frac{i}{\hbar}Et}=-A\frac{iE}{\hbar}e^{-\frac{i}{\hbar}(Et-xp)}=-\frac{iE}{\hbar}\psi$

$E\psi=i\hbar\frac{\partial\psi}{\partial t}\; \; \; \; \; \; \; \; 55$

As for $p^{2}\psi$ , we find the the 2^nd-order partial derivative of $\psi$ with respect to $x$ :

$\frac{\partial^{2}}{\partial x^{2}}Ae^{-\frac{i}{\hbar}(Et-xp)}=Ae^{-\frac{i}{\hbar}Et}\frac{\partial^{2}}{\partial x^{2}}e^{\frac{i}{\hbar}xp}=\left ( \frac{i}{\hbar}p\right )^{2}Ae^{-\frac{i}{\hbar}(Et-xp)}=-\frac{p^{2}}{\hbar^{2}}\psi$

$p^{2}\psi=-\hbar^{2}\frac{\partial^{2}\psi}{\partial x^{2}}\; \; \; \; \; \; \; \; 56$

Substituting eq55 and eq56 in eq54, we have

$i\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^{2}}{2m}\frac{\partial^{2}\psi}{\partial x^{2}}+V\psi\; \; \; \; \; \; \; \; 57$

Eq57 is the one-particle, one-dimensional, time-dependent Schrodinger equation, which has the general solution $\psi(x,t)=\psi(x)e^{-\frac{i}{\hbar}Et}$ .

Question

Show that $\psi(x,t)=\psi(x)e^{-\frac{i}{\hbar}Et}$ is a solution to eq57.

Answer

For LHS of eq57

$i\hbar\frac{\partial\psi(x,t)}{\partial t}=-i\hbar\psi(x)i\frac{E}{\hbar}e^{-i\frac{Et}{\hbar}}=E\psi(x,t)$

So,

$\left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2}}{\partial x^{2}}+V\right ]\psi(x,t)=E\psi(x,t)$

One-particle, time-dependent Schrodinger equation

Question

Answer

Next article: classical angular momentum

Previous article: 1-D classical wave equation

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply