Hilbert space

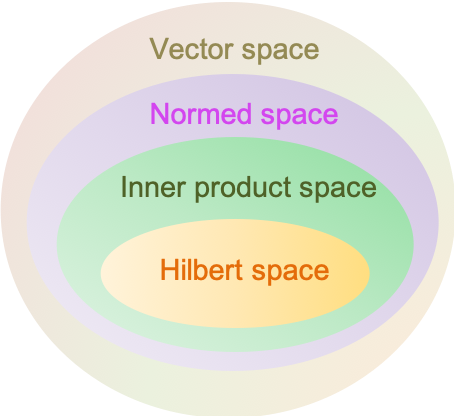
A Hilbert space $H$ is a complete inner product space. It allows the application of linear algebra and calculus techniques in a space that may have an infinite dimension.

The inner product in a Hilbert space has the following properties:

Conjugate symmetry: $\langle\phi_1\vert\phi_2\rangle=\langle\phi_2\vert\phi_1\rangle^{*}$
Linearity with respect to the 2^nd argument: $\langle\phi_1\vert c_2\phi_2+c_3\phi_3\rangle=c_2\langle\phi_1\vert \phi_2\rangle+c_3\langle\phi_1\vert \phi_3\rangle$
Antilinearity with respect to the first argument: $\langle c_1\phi_1+c_2\phi_2\vert \phi_3\rangle=c_1^{*}\langle\phi_1\vert \phi_3\rangle+c_2^{*}\langle\phi_2\vert \phi_3\rangle$
Positive semi-definiteness: $\langle\phi_1\vert \phi_1\rangle\geq 0$ , with $\langle\phi_1\vert \phi_1\rangle= 0$ if $\phi_1=0$

The last property can be illustrated using the $\mathbb{R}^{2}$ space that is equipped with an inner product. Such a space is an example of a real finite-dimensional Hilbert space. The inner product of the vector $\boldsymbol{\mathit{u}}$ with itself is:

$\boldsymbol{\mathit{u}}\cdot\boldsymbol{\mathit{u}}=\begin{pmatrix} u_1 &u_2 \end{pmatrix}\begin{pmatrix} u_1\\u_2 \end{pmatrix}=u{_{1}}^{2}+u{_{2}}^{2}=\{\begin{matrix} >0 &if\; \boldsymbol{\mathit{u}}\neq 0 \\ 0&if \; \boldsymbol{\mathit{u}}=0\end{matrix}$

We define a complete Hilbert space as one where every Cauchy sequence in $H$ converges to an element of $H$ . If you recall, a Cauchy sequence is a sequence, e.g. $\left \{ x_n \right \}_{n=1}^{\infty}$ where $x_n=\sum_{k=1}^{n}\frac{(-1)^{k+1}}{k}$ , for which

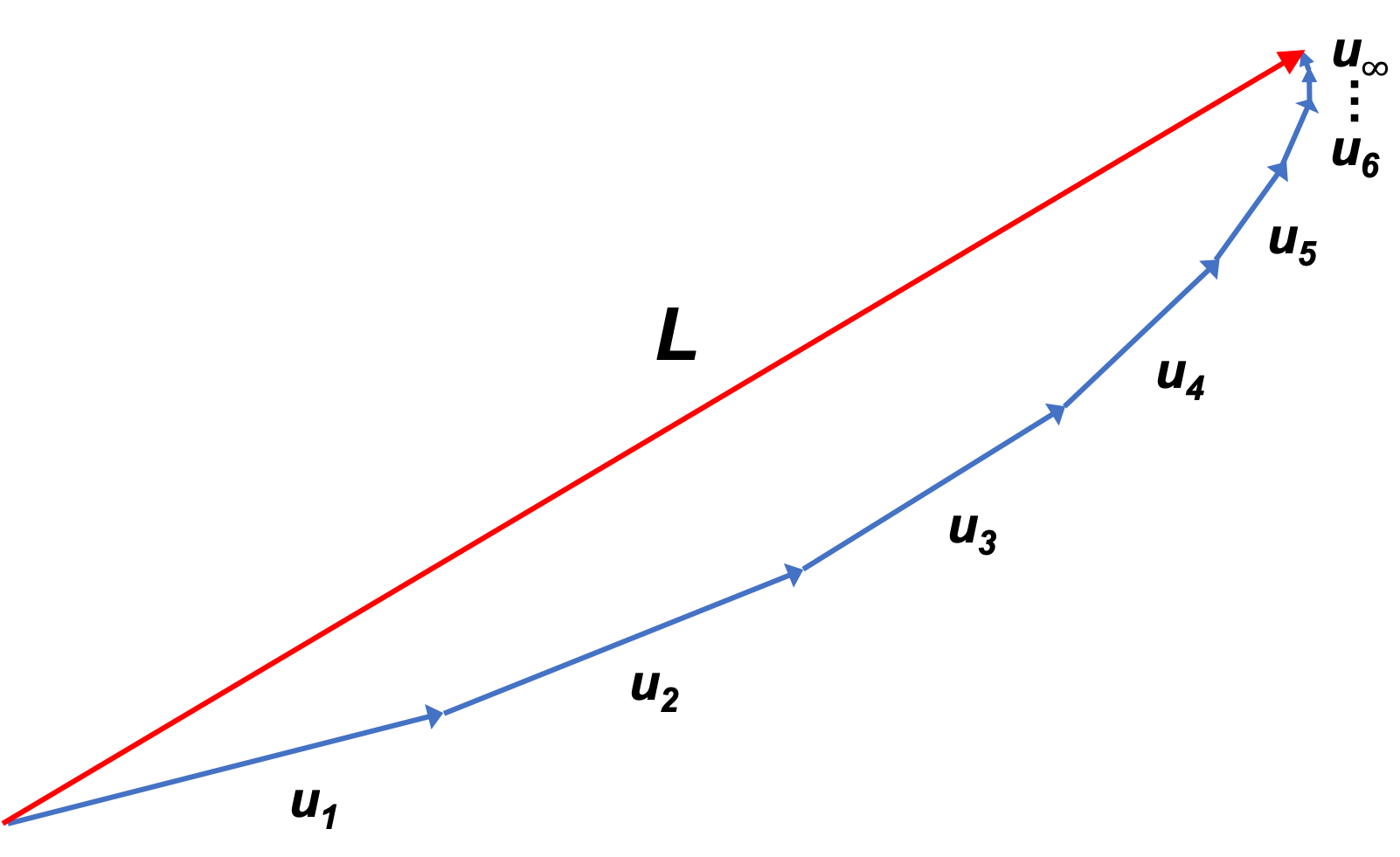
$\lim_{m,n\rightarrow \infty}\left | x_n-x_m \right |=0$

We can also define the completeness of a Hilbert space in terms of a sequence of vectors $\left \{ \boldsymbol{\mathit{v_n}} \right \}_{n=1}^{\infty}$ , where $\boldsymbol{\mathit{v_n}} =\sum_{k=1}^{n}\boldsymbol{\mathit{u_k}}$ . Each element $\boldsymbol{\mathit{v_n}}$ is represented by a series of vectors, which converges absolutely (i.e. $\sum_{k=1}^{\infty}\left \| \boldsymbol{\mathit{u_k}} \right \|< \infty$ ) and converges to an element of $H$ . In other words, the series of vectors in $H$ converges to some limit vector $\boldsymbol{\mathit{L}}$ in $H$ :

$\lim_{n\rightarrow \infty}\left \|\boldsymbol{\mathit{L}}-\sum_{k=1}^{n}\boldsymbol{\mathit{u_k}} \right \|=0$

Generally, every element of a vector space can be a point, a vector or a function. In quantum mechanics, we are interested in a Hilbert space called the $L^{2}$ space, where the eigenfunctions of a Hermitian operator are square integrable, i.e. $\int_{-a}^{b}\left | \phi(x) \right |^{2}dx< \infty$ .

Not to be confused with the completeness of a Hilbert space, the completeness of a set of basis eigenfunctions refers to the property that any eigenfunction of the Hilbert space can be expressed as a linear combination of the basis eigenfunctions. An example is the $\mathbb{R}^{2}$ space, where the set of basis vectors $\left \{\boldsymbol{\mathit{\hat i}},\boldsymbol{\mathit{\hat j}}\right \}$ is complete, with a linear combination of $\boldsymbol{\mathit{\hat i}}$ and $\boldsymbol{\mathit{\hat j}}$ spanning $\mathbb{R}^{2}$ . In $H$ , the number of basis vectors $\boldsymbol{\mathit{u_k}}$ may be infinite. If the set of $\boldsymbol{\mathit{u_k}}$ is complete, we say that it spans $H$ , which is itself complete.

Just as the orthonormal vectors $\boldsymbol{\mathit{\hat i}}$ and $\boldsymbol{\mathit{\hat j}}$ form a complete set of basis vectors in the $\mathbb{R}^{2}$ space, where any vector in $\mathbb{R}^{2}$ can be expressed as a linear combination of $\boldsymbol{\mathit{\hat i}}$ and $\boldsymbol{\mathit{\hat j}}$ , we postulate the existence of a complete basis set of orthonormal wavefunctions of any Hermitian operator in $L^{2}$ .

Next article: Kronecker product

Previous article: completeness of a space

Content page of quantum mechanics

Content page of advanced chemistry

Main content page

Leave a Reply Cancel reply