Category: Intermediate Chemistry

Posted on

Millikan’s oil drop experiment: overview

Robert Millikan conducted an experiment in 1909 to measure the charge of an electron. He devised an apparatus to observe electrically-charged droplets of oil between two horizontal plates that had a potential difference of several thousand volts applied across them.

The oil droplets were sprayed from an atomiser into an upper chamber. In the space between the plates, the air were ionised by X-rays, causing the oil droplets to acquire electrons and become negatively charged as they fell and traversed through the air between the plates. Millikan then performed a few tasks and observed the motion of the oil droplets through a microscope.

 

Next ArTicle: Task 1
Content page of millikan’s oil drop experiment
Content page of intermediate chemistry
Main content page
Posted on

Millikan’s oil drop experiment: task 1

Millikan’s oil drop experiment consists of a few tasks.

For a start, the power supply to the plates is cut off (V = 0). The oil-droplets falling between the plates accelerate due to the effect of gravitational force and then continue downwards at terminal velocity as they encounter increasing air resistance. The three forces acting on an oil droplet are:

Gravitational force,

Fg

 The force of attraction between the mass of the earth and that of the oil droplet.
Upthrust (buoyant),

Fu

 The force exerted by a liquid or a gas on a body when the body displaces some weight of the liquid or gas. It is due to the pressure difference between the top and bottom of the object (as a result of the collision of liquid or gas molecules with the body from the top and bottom) and equal to the weight of the liquid or gas displaced.
Drag (viscous),

Fd

 The force caused by relative motion (friction) between an object and a liquid or gas. It is proportional to the velocity of the object, the radius of the object and the viscosity of the liquid or gas.

 

At terminal velocity,

F_{g}=F_{d}+F_{u}\; \; \; \; \; \; \; (1)

The oil droplet is assumed to be spherical. So, Fg, the weight of the oil droplet, is:

F_{g}=mg=\frac{4\pi }{3}r^{3}\rho g\; \; \; \; \; \; \; (2)

where m, ρ and r are the mass, density and radius of the oil droplet, respectively.

The equation of the drag force acting on the oil droplet can be expressed using Stokes’ law:

F_{d}=6\pi r\eta v_{1}\; \; \; \; \; \; \; (3)

where v1, is the terminal velocity of the falling oil droplet and η is the viscosity of air.

Through the microscope, Millikan recorded the distance travelled by the falling oil droplet over a period of time and calculated the terminal velocity v1.

For a perfectly spherical oil droplet the upthrust acting on it is:

F_{u}=mg=\frac{4\pi }{3}r^{3}\rho _{air}g\; \; \; \; \; \; \; (4)

where ρair is the density of the air.

Substituting eq2, eq3 and eq4 in eq1 yields

6\pi r\eta v_{1}=\frac{4\pi }{3}r^{3}(\rho -\rho _{air})g\; \; \; \; \; \; \; (5)

r=\sqrt{\frac{9\eta v_{1}}{2g(\rho -\rho _{air})}}\; \; \; \; \; \; \; (6)

NEXT ARTICLE: TASK 2
Previous article: Overview
Content page of millikan’s oil drop experiment
Content page of intermediate chemistry
Main content page
Posted on

Millikan’s oil drop experiment: task 2

The power supply to the plates is turned back on and the electric force acting on the oil droplet is:

F_{e}=qE\; \; \; \; \; \; \; (7)

where q is the charge on the oil droplet and E is the electric field between the plates.

For parallel plates,

E=\frac{V}{d}\; \; \; \; \; \; \; (8)

where V is the potential difference across the plates and d is the distance between the plates.

Combining eq7 and eq8,

q=\frac{F_{e}\: d}{V}\; \; \; \; \; \; \; (9)

If V is adjusted until the oil droplet remained stationary,

F_{e}=mg\; \; \; \; \; \; \; (10)

Combining eq9 and eq10,

q=\frac{mgd}{V}

Our objective is to determine the value of q, but it is difficult to accurately measure m. Therefore, we have to carry out another task.

 

NEXT ARTICLE: TASK 3
Previous article: task 1
Content page of millikan’s oil drop experiment
Content page of intermediate chemistry
Main content page
Posted on

Millikan’s oil drop experiment: task 3

Next, V is turned up slightly so that the oil droplet rises with a new terminal velocity v2.

We have:

F_{e}+F_{u}=F_{d}+F_{g}\; \; \; \; \; \; \; (11)

Note that the electric force is acting upwards (since the oil droplet is rising); upthrust is also acting upwards (because the pressure is still greater below the object than above it due to the exponential distribution of air); drag is now acting downwards because the oil droplet is rising, and weight continues to act downwards due to the effect of gravitational force. Substituting eq2, eq3 (with v2 instead of v1), eq4 and eq7 in eq 11 yields

qE+\frac{4\pi }{3}r^{3}\rho _{air}g=6\pi \eta rv_{2}+\frac{4\pi }{3}r^{3}\rho g

qE-\frac{4\pi }{3}r^3(\rho -\rho _{air})g=6\pi \eta rv_{2}\; \; \; \; \; \; \; (12)

Substituting eq5 in eq12 gives

qE-6\pi r\eta v_{1}=6\pi \eta rv_{2}\; \; \; \; \; \; \; (13)

Substituting eq8 in eq13 and rearranging results in

q=\frac{6\pi r\eta (v_{1}+v_{2})d}{V}\; \; \; \; \; \; \; (14)

Once again, Millikan recorded the distance travelled by the rising oil droplet over a period of time and calculated the new terminal velocity, v2.

Substituting the values of v1, v2 and the calculated value of r (from eq6) in eq14, Millikan determined a value for q. He repeated the experiment multiple times, each time varying the strength of X-rays ionizing the air, resulting in a varying number of electrons attaching to the oil droplet. He then obtained various values of q and found them to be multiples of 1.5924 x 10-19 C. Millikan concluded that the value of 1.5924 x 10-19 C is equal to the charge of a single electron. Subsequent determinations refined that value to 1.602176487 x 10−19 C.

Using the Faraday constant and the value of the charge of a single electron that he determined, Millikan calculated the Avogadro constant and proved that one Faraday is the quantity of charge for one mole of electrons.

 

Previous article: task 2
Content page of millikan’s oil drop experiment
Content page of intermediate chemistry
Main content page
Posted on

Mass spectrometry: the mechanics

Mass spectrometry in the early days focuses on determining the charge-to-mass ratio, e/m, of an electron. This involves a few steps, beginning with the electric field turned on and the magnetic field turned off. The diagram below shows the mechanics of the electrons as they pass through the electric field plates.

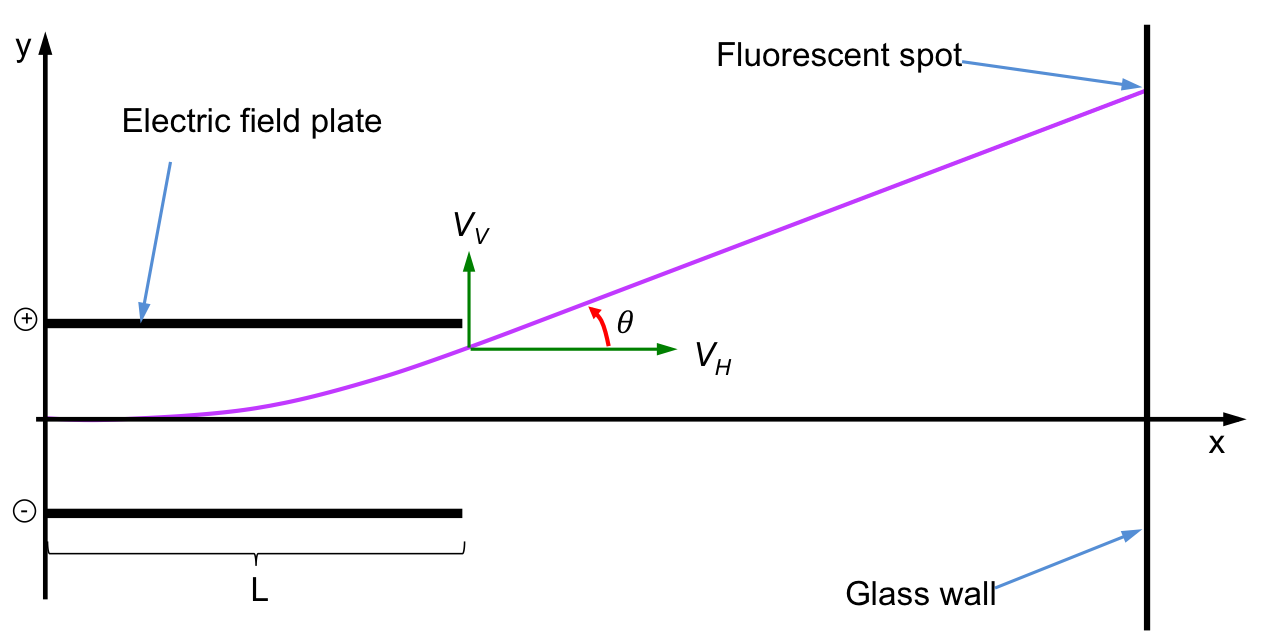
An electric force, Fe, acts on an electron with charge, e, passing through the electric field, E, in the x-direction where

F_{e}=eE\; \; \; \; \; \; \; (1)

and gives the electron with mass, m, an acceleration, a:

F_{e}=ma\; \; \; \; \; \; \; (2)

Combining eq1 and eq2,

a=\frac{eE}{m}\; \; \; \; \; \; \; (3)

As the electric force acts only in the y-direction, the velocity of the electron in the x-direction remains constant at vH. The velocity of the electron in the y-direction, vV, is zero at the point where it enters the electric field and increases to a maximum value at the point where the electron leaves the electric field. This maximum value of vV remains constant after the electron exits the electric field and is given by:

v_{V}=\frac{dS}{dt}=\frac{d(ut+\frac{1}{2}at^{2})}{dt}=at

where S is the displacement of the electron in the y-direction, u is the initial velocity of the electron in the y-direction before entering the electric field (i.e. u = 0) and t is the time during which the electric force acts on the electron.

In other words, t is the time taken for the electron to travel the length of the electric field plate, L. Therefore,

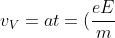v_{V}=at=(\frac{eE}{m})(\frac{L}{v_{H}})\; \; \; \; \; \; \; (4)

The trigonometric relationship between vH and vV after the electron leaves the electric field is:

tan\theta =\frac{v_{V}}{v_{H}}=\frac{eEL}{{v_{H}}^{2}m}\; \; \; \; \; \; \; (5)

The electric field strength is adjusted so that the angle of deflection is small. Therefore, tanθ ≈ θ and eq5 becomes,

\theta =\frac{eEL}{{v_{H}}^{2}m}\; \; \; \; \; \; \; (6)

The value of θ is recorded, leaving vH  as the only unknown variable (in eq6) for the calculation of e/m. To determine vH , the magnetic field, B, is turned on while the electric field is still on. Using Fleming’s left hand rule, the magnetic force, FB, acts on the electron (at the point when the electron just enters the magnetic field from the left side) and deflects it in the negative y-direction:

F_B=ev_HB\; \; \; \; \; \; \; \; (7)

The magnetic field is then adjusted to the extent that the angle of deflection of the cathode ray is zero, meaning Fe = FB. Substituting eq1 and eq7 in Fe = FB, we have:

v_{H}=\frac{E}{B}\; \; \; \; \; \; \; (8)

Substitute eq8 in eq6

\frac{e}{m}=\frac{E\theta }{B^{2}L}\; \; \; \; \; \; \; (9)

The values of all the variables on the right hand side of eq9 are now known and the charge-to-mass ratio e/m of the electron can be determined. The magnitude of e/m that Thomson obtained ranged from 0.7 x 1011 C/kg to 2 x 1011 C/kg. The currently accepted value is 1.758820024 x 1011 C/kg.

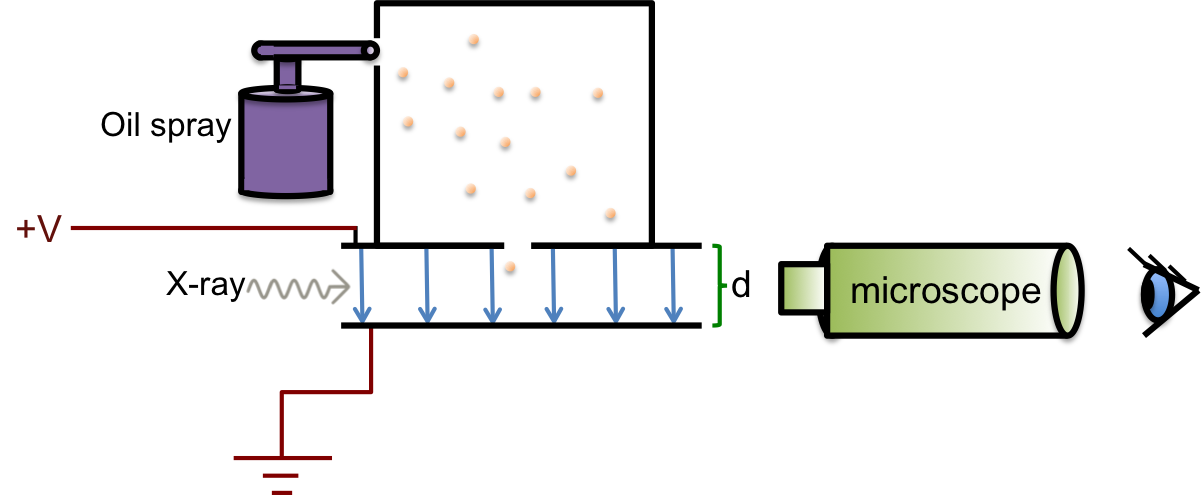
Finally, in 1909, when Robert Millikan determined the charge of an electron via his famous oil drop experiment, the estimated mass of an electron was calculated.

 

next article: application, relative isotopic mass
Previous ArTicle: J.J. thomson’s cathode ray experiment
Content page of mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

Application of mass spectrometry: relative isotopic mass

A mass spectrometer measures the mass of an isotope relative to that of carbon-12 by analysing the ratio of the ionised isotope’s deflection to the ionised carbon-12’s deflection.

From eq9, we have:

\frac{e_{isotope}}{m_{isotope}}=\frac{E\theta _{isotope}}{B^{2}L}\; \; \; \; \; \; \; (10)

\frac{e_{^{12}C}}{m_{^{12}C}}=\frac{E\theta _{^{12}C}}{B^{2}L}\; \; \; \; \; \; \; (11)

Assume both ions are univalent so that e_{^{12}C}=e_{isotope} and divide eq11 by eq10:

\frac{m_{isotope}}{m_{^{12}C}}=\frac{\theta _{^{12}C}}{\theta _{isotope}}\; \; \; \; \; \; \; (12)

Therefore,

mass\; of\; isotope=\frac{\theta _{^{12}C}}{\theta _{isotope}}m_{^{12}C}\; \; \; \; \; \; \; (13)

We can also represent eq13 in the form

mass\; of\; isotope=\frac{m_{isotope}/z_{isotope}}{m_{^{12}C}/z_{^{12}C}}m_{^{12}C}\; \; \; \; \; \; \; (14)

where we have replaced e with the notation z. The output of eq14 is a value with unit of unified atomic mass unit, u, since the ratio is unit-less while m_{^{12}C}=12u.

Finally, we divide the output of eq14 by 1u to obtain the relative isotopic mass, which is a dimensionless quantity that is defined as the ratio of the mass of an isotope in unified atomic mass unit to one unified atomic mass unit.

 

Question

Is it possible to accurately measure the mass of an atom in kg using eq9 without a reference isotope?

Answer

No. Due to the limits of precision engineering, measurements of the mass of an atom in kg by directly applying eq9 differ from one mass spectrometer to another. We therefore need a reference ‘flight path’ that we can compare with, i.e. using eq14. Since the value of m_{^{12}C} is accurately defined in u, the output of eq19 must be in unified atomic mass unit. The value in kg is then obtained by the following conversion:

1u = 1.660539 x 10-27 kg

 

Next ArTicle: Modern mass spectrometer design
Previous ArTicle: the mechanics
Content page of Mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

J. J. Thomson’s cathode ray experiment

Mass spectrometry is an analytical technique that utilises an instrument called a mass spectrometer to identify and quantify ions based on their mass-to-charge ratios. J. J. Thomson, an English physicist, constructed one of the earliest mass spectrometers (see diagram below) and demonstrated in an experiment in 1897 that atoms are made of subatomic particles called electrons. Using the spectrometer, he determined the charge-to-mass ratio of an electron.

The ioniser on the left of the spectrometer is not a complete vacuum; it is filled with a trace amount of air molecules, which are always in equilibrium between their neutral and ionic forms due to natural occurring processes like photoionisation. Consequently, free electrons are present among the trace amount of air molecules in the ioniser.

N_{2}(g)\overset{uv}{\rightleftharpoons}{N_{2}}^{+}(g)+e^{-}

Instead of producing electrons from the cathode via a heated filament, the ioniser operates on the principle of a ‘cold cathode’, where a high potential difference maintained between the cathode and anode accelerates the free electrons present in the trace amount of air. These electrons collide with other gas molecules and knock more electrons off them, creating a cascade of ions and electrons called a Townsend discharge. The electrons are attracted towards the anode, where they are focused into a beam called a cathode ray and continue their path to the electric field plates and electromagnet, where they are deflected.

When the electrons eventually strike the atoms in the glass at the right end of the spectrometer, they excite electrons intrinsic to the atoms to a higher energy state. When these excited electrons relax back to the ground state, they emit light in the form of fluorescence, and the angle of deflection, θ, can be read from the fluorescent spot on the scale.

By working out the mechanics of the trajectory of the cathode ray, Thomson managed to calculate the charge-to-mass ratio of an electron and concluded that the negatively charged ‘corpuscles’ (the term he used at the time for electrons) must have originated from the dissociation of trace amounts of gas molecules. This conclusion was based on the fact that the charge-to-mass ratio of a corpuscle is about 1,800 times greater than that of a charged hydrogen atom (the charge-to-mass ratio of a hydrogen ion had been investigated earlier).

next article: The mechanics
Content page of Mass spectrometry
Content page of intermediate chemistry
Main content page
Posted on

Perrin’s experiment: details of the experiment

Perrin needed to prove that NA is a constant in the following equation that he derived:

\frac{N'}{N}=e^{-\frac{N_{A}mgh}{RT}}\; \; \; \; \; \; \; (9)

The challenge was that N’, N and m could not be measured directly. He circumvented this issue by replacing the gas in the cylinder with visible particles suspended in a liquid. Drawing from the principles of Brownian motion, Perrin assumed that collisions between liquid molecules and the visible particles would result in a distribution similar to that of gas molecules in the cylinder. He also assumed that the motion of the particles obeyed the ideal gas law.

Perrin used a monodisperse colloid of a gum called gamboge, consisting of thousands of gamboge spheres in a water cylinder. He studied the distribution of the spheres with a microscope and adjusted eq9 to account for the upthrust of water on the gamboge spheres. For a single gamboge sphere (“particle”),

upthrust = weight of liquid displaced = ml g = dVl g                (10)

where ml is the mass of the liquid displaced, d is the density of the liquid and Vl is the volume of the liquid displaced.

Furthermore, the volume of liquid displaced is equal to the volume of the particle, Vp :

Vl = Vp                (11)

Substituting eq11 in eq10 yields

upthrust = dVp g               (12)

Since Vp = m/D, where m is the mass of a particle and D is the density of the particle, eq 12 becomes:

upthrust=\frac{d}{D}mg\; \; \; \; \; \; \; (13)

The effective weight of the particle is therefore the difference between the weight of the particle and the upthrust on the particle:

effective\; weight\; of\; a\; particle=mg-\frac{d}{D}mg

Replacing the weight mg of a gas molecule in eq9 with the effective weight of a suspended particle gives

\frac{N'}{N}=e^{-\frac{N_{A}mg(1-\frac{d}{D})h}{RT}}\; \; \; \; \; \; \; (14)

The suspended particles must be heavier than the liquid molecules for the particles to exert a downward pressure on the liquid, producing an upthrust that results in a lower effective weight for the particles. This means that d < D for eq14 to be valid. Hence, the choice of particle material is important.

Perrin meticulously prepared emulsions containing particles that were equal in size. He calculated the average mass of a particle by weighing a specified number of particles, determined its density using various methods (including the specific gravity bottle method), and counted the number of suspended particles per unit volume at different heights using a microscope.

After repeating the experiment with different particle materials (e.g. mastic), sizes, masses, liquids and temperatures, he found that the value of NA remained fairly constant, reporting numbers ranging from 6.5 x 1023 to 7.2 x 1023. He further conducted experiments using methods based on radioactivity, blackbody radiation and the motion of ions in liquids, obtaining very similar results for the value of NA. Perrin concluded that the results justified the hypotheses that had guided him, including Avogadro’s law, and named the constant the Avogadro constant, in honour of Avogadro.

The accuracy of the value of the Avogadro constant was subsequently improved by other scientists, one of whom was Robert Millikan.

Previous ArTicle: the concept
Content page of Perrin’s experiment
Content page of intermediate chemistry
Main content page
Posted on

Perrin’s experiment: the concept

Perrin developed the concept to analyse the vertical distribution of a volume of molecules of an ideal gas, with total mass of mc, in a cylinder with a cross-sectional area A and small height h at temperature T. Firstly, he considered an infinitesimal layer of the gas with mass dmc and thickness dh in the cylinder.

This layer of gas experiences an upward force Fu = pA from the pressure exerted by the gas it, and a downward force Fd = gdmc + (p+dp)A due to the gravitational force and the pressure exerted by the gas above it. At equilibrium, Fu = Fd and we get:

dp=-\frac{g}{A}dm_{c}\; \; \; \; \; \; \; \; (3)

At this juncture, Perrin, with reference to the works of previous scientists (Avogadro, Dalton, etc.) on relative mass of molecules and introduced an important definition:

A gramme-molecule, M, is the mass of a gas that occupies the same volume as 2g of hydrogen gas at the same temperature and pressure*

* Perrin’s definition of the gramme-molecule is somewhat similar to the 1967 definition of the mole. This definition, together with Avogadro’s law, implies that a gramme-molecule of gas X and a gramme-molecule of gas Y have the same number of molecules.

With Perrin’s definition, the physical state of the gas in the cylinder can be described using the ideal gas law (eq2), where the amount of gas n is expressed in multiples of gramme-molecule M:

p(Adh)=\frac{dm_{c}}{M}RT\; \; \; \; \; \; \; (4)

Substituting eq4 in eq3 by eliminating dmc/A yields

\frac{1}{p}dp=-\frac{Mg}{RT}dh\; \; \; \; \; \; \; (5)

The expression for the distribution of the gas in the entire cylinder can be obtained by integrating both sides of eq5 (see above diagram):

\int_{p}^{p'}\frac{1}{p}\: dp=-\frac{Mg}{RT}\int_{0}^{h}dh

\frac{p'}{p}=e^{-\frac{Mgh}{RT}}\; \; \; \; \; \; \; (6)

From eq2, we have p’ = n’RT/V’ and p = nRT/V. Substituting these two equations in eq6 gives

\frac{N'}{N}=e^{-\frac{Mgh}{RT}}\; \; \; \; \; \; \; (7)

where N’ = n’/V’ and N = n/V; that is, the number densities of the gas at the upper and lower levels of the cylinder.

Furthermore, the gramme-molecule of the gas, M, is equal to the number of molecules in a gramme-molecule, NA, multiplied by the mass of a molecule of the gas, m:

M=N_{A}m\; \; \; \; \; \; \; (8)

Substituting eq8 in eq7 results in

\frac{N'}{N}=e^{-\frac{N_{A}mgh}{RT}}\; \; \; \; \; \; \; (9)

If Avogadro’s hypothesis – that ‘equal volumes of all gases at the same temperature and pressure have the same number of molecules’ – is true, NA in eq9 must be constant for different ideal gases. To determine the value of NA, Perrin would need to (i) count the number of molecules per unit volume at the upper and lower levels of the cylinder (of fixed height, h, at a constant temperature, T) for a particular gas, (ii) repeat the count for other gases with different m, and  (iii) calculate the average value of NA. However, a problem arose.

 

next article: The experiment
Previous ArTicle: John perrin
Content page of Perrin’s experiment
Content page of intermediate chemistry
Main content page
Posted on

Jean Perrin

Jean Perrin, a French scientist, was one of the earlier researchers who attempted to determine the Avogadro constant.

Who inspired Perrin?

Prior to Perrin’s work in 1909, Amedeo Avogadro, an Italian scientist, published papers between 1811 and 1841 and suggested that

Equal volumes of all gases at the same temperature and pressure have the same number of molecules

This became known as Avogadro’s law. It implies that for a given mass of an ideal gas at constant temperature and pressure, the volume V of the ideal gas is directly proportional to its amount n:

V = kn                 (1)

where k is the proportionality constant.

When eq1 is incorporated into the combined gas law, which was developed many years earlier, we have the ideal gas law:

pV = nRT                 (2)

At that time, n was known as ‘amount of gas’ rather than ‘number of moles’, as the mole concept had not yet been developed. Since the amount of gas can be in measured in different ways, the gas constant R had different units back then. 

Avogadro also investigated the relative mass of different gases; for example, he deduced from gas density data that the relative molecular weight of nitrogen and hydrogen is in the ratio of 13.2 : 1 and that the ratio of oxygen molecules and hydrogen molecules in water is 0.5 : 1.

Lastly, the research of botanist Robert Brown in 1872, which involved the random motion of particles suspended in a liquid or a gas due to their collisions with the surrounding molecules, also played an important role in Perrin’s calculations.

next article: The concept
Content page of Perrin’s experiment
Content page of intermediate chemistry
Main content page
Mono Quiz