In chemical thermodynamics, the universe is composed of a system and its surroundings. The system is a part of the universe that is being studied, while its surroundings is the remaining part of the universe, with the two regions separated by a boundary. For example, if we are studying a gaseous reaction in a closed vessel in thermal equilibrium with its surroundings, the system is the gas in the vessel, while its surroundings is the space outside the vessel, and the boundary is the thermally conducting vessel walls (see diagram below).
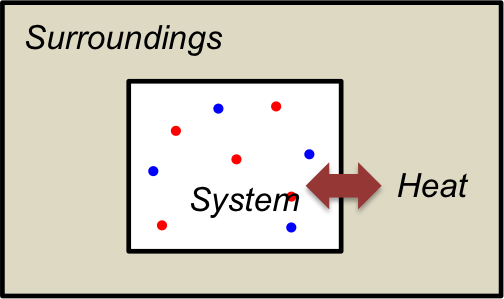
The change in entropy of the universe is given by the sum of the change in entropy of the system and the change in entropy of the surroundings:

or under standard conditions:

The change in entropy of the universe is sometimes called the total entropy change ΔStoto. However, we are mostly concerned about chemical reactions that are usually defined as occurring within a system, and especially whether such reactions are spontaneous. To determine the spontaneity of a reaction using eq3, we need to know the following facts:
This means that we require, in addition to ΔSsyso, the value of ΔSsuro, which may not be easily available. To circumvent this problem, we seek a new measure, which can be developed as follows:
For a reaction carried out under standard conditions, ΔSsyso is given by eq1 of the previous article, i.e., the standard reaction entropy of the system, ΔSro, while

where T is the temperature of the surroundings, which is equal to the temperature of the system, as the system is at thermal equilibrium with its surroundings.
Although the derivation of eq4 requires knowledge of chemical thermodynamics at the advanced level, we can interpret it by, firstly, noting that the change in enthalpy of the surroundings at constant pressure is equivalent to the amount of heat transferred from the system to the surroundings. We also mentioned in the previous article that an increase in entropy of a system is associated with an increase in number of moles of substances. Rearranging eq4, we get

We can say that the ‘spread’ of a given value of ΔHsuro (for a reaction occurring in the surroundings) over a larger increase in the number of moles of substances (i.e. a higher value of ΔSsuro) leads to lower energy per particle and hence, lower T.
Having interpreted eq4, let’s consider an exothermic reaction occurring in the system that releases thermal energy that is measured as the change in enthalpy of the system, ΔHsyso. Since the system’s vessel walls are thermally conducting, by the theory of conservation of energy, energy transferred from the system to its surroundings increases the energy of the surroundings and decreases the energy of the system, i.e.,

Substituting eq6 in eq4,

Substituting eq7 in eq3,

From the previous article, we know that a reaction occurring in a system can result in either positive or negative ΔSsyso. Furthermore, we mentioned earlier that:
-
- ΔSunio > 0 for a spontaneous reaction
- ΔSunio = 0 when a reaction reaches equilibrium, where there is no net transfer of thermal energy between a system and its surroundings.
Therefore, with reference to eq8, if the reaction is exothermic and ΔHsyso is large and negative to the extent that ΔSunio > 0, the reaction is spontaneous. For an endothermic reaction to be spontaneous, ΔSsyso must be positive enough to compensate for the term  .
.
Substituting eq1 from the previous article and eq7 in eq3,
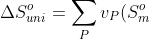_P-\sum_Rv_R(S_m^o)_R-\frac{\Delta&space;H_{sys}^o}{T}\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;\;&space;9)

Question
Calculate ΔSuni for the reaction BaCO3(s) → BaO(s) + CO2(g) at 25°C and 1500°C given Smo[BaCO3(s)] = 112.1 JK-1mol-1, Smo[BaO(s)] = 70.4 JK-1mol-1, Smo[CO2(g)] = 213.6 JK-1mol-1 and ΔHsyso = 269.0 kJmol-1.
Answer
At 25°C, using eq9,

Since ΔSuni < 0, the reaction is not spontaneous. This is consistent with the fact that barium carbonate is thermodynamically stable at room temperature.
At 1500°C, if we assume ΔHsyso and the standard absolute molar entropies remain unchanged,
=70.4+213.6-112.1-\frac{269000}{1798.15}=22.3\,&space;JK^{-1}mol^{-1})
The decomposition of barium carbonate becomes spontaneous at this elevated temperature.
Eq8 is a better way to measure the spontaneity of a reaction, as it only requires the calculation of thermodynamic properties of the system. In fact, we can generate a new measure (a new function) in place of ΔSunio to determine the spontaneity of a reaction, starting from:

Multiplying eq10 throughout by T,


or

where ΔGsyso = ΔHsyso – TΔSsyso.
We call this function, ΔGsyso, the Gibbs energy of the system.
Finally, just as ΔSunio = 0 when a reaction reaches equilibrium, where there is no net transfer of thermal energy between a system and its surroundings, ΔGsyso = 0 for a reaction at equilibrium.
, we can define the standard reaction Gibbs energy as:
.

, and the standard reaction entropy of a system is
, the standard reaction Gibbs energy of a system is:
and
as well as those in
and
cancel out when we compute ΔGro and ΔHro respectively (see sections on standard enthalpy change of formation and Hess Law for details).

given ΔGfo[C2H2(g)] = -32.9 kJmol-1, ΔGfo[CO2(g)] = -394.4 kJmol-1 and ΔGfo[H2O(l)] = -237.2 kJmol-1.