Category: Intermediate Chemistry

Posted on

Analysing rate data (chemical kinetics)

The aim of analysing rate data from an experiment is to determine the reaction order with respect to different reactants, the rate constant, and hence the rate law.

Although various approaches can be employed to achieve this, depending on the type of reaction being investigated, most experimental procedures are structured in a way that narrows the approaches down to one or two.

The commonly used methods for analysing rate data are:

    1. the half-life method
    2. the differential method
    3. the integral method
    4. the initial rate method; and
    5. the isolation method

Some experiments may require a combination of these methods to derive the rate equation. We shall look at them individually and see how they can be used.

 

Next article: Half-life method
Previous article: Monitoring the progress of a reaction
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Half-life method

The half-life method for analysing rate data is useful when the rate law involves a single reactant, i.e.

rate=k[A]^i\; \; \; \; \; \; \; \; 22

To determine the values of k and i, we let the reaction proceed, measure the appropriate physical property and plot the data in a concentration versus time graph.

If the curve is a straight line (see graph above), the gradient or the change in concentration versus the change in time (i.e. rate of reaction) is a constant. This implies that i = 0 in eq22, i.e. a zero order reaction. We can further confirm this by finding the first three successive half-lives from the graph (there is no need to consider the subsequent half-lives) and substitute them, along with the initial concentration of the reactant, in eq20 from the article on half-life: t_{\frac{1}{2}}=\frac{[A]_0}{2k}. The three substitutions should give three different values of k that should be close to one another. The average of these values of k is then taken to give the rate equation: rate = kave.

If the curve is concave (see diagram above), it represents a higher order reaction. Similarly, the first three successive half-lives is determined from the graph. If the values are relatively constant, the graph corresponds to a first order reaction, with i = 1. The value of the rate constant is then found using eq19 from the article on half-life: t_{\frac{1}{2}}=\frac{ln2}{k}, resulting in the rate equation: rate = k[A].

If the half-lives are very different from one another, they could be those of a second order reaction, i = 2. We can verify this by substituting the three half-life values, along with the initial concentration of the reactant, in eq21 from the article on half-life: t_{\frac{1}{2}}=\frac{1}{k[A]_0}, which should give three different values of k that may be close to one another. The average value of the rate constant can be found and hence, the rate equation: rate = kave[A]2.

 

Next article: Differential method
Previous article: Analysing rate data
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Differential method (rate laws)

The differential method of determining the rate of a reaction makes use of the differential form of a rate law.

Just like the half-life method, the differential method is useful for reactions involving a single reactant, e.g.

N_2O_5(g)\rightleftharpoons 2NO_2(g)+\frac{1}{2}O_2(g)

where we can write the rate equation as

-\frac{d[N_2O_5]}{dt}=k[N_2O_5]^i\; \; \; \; \; \; \; \; 23

Taking the natural logarithm on both sides of eq23, we have

ln\left [ -\frac{d[N_2O_5]}{dt} \right ]=iln[N_2O_5]+lnk\; \; \; \; \; \; \; \; 24

To find the rate constant, k, and the order, i:

    1. Run the experiment in a rigid vessel and record the concentrations of N2O5 using spectroscopic methods at various times.
    2. Plot a graph of [N2O5] versus time.
    3. Find the gradients to the curve at selected concentrations; that is, find \frac{d[N_2O_5]}{dt} at various [N2O5].
    4. With reference to eq24, plot a graph of ln\left [- \frac{d[N_2O_5]}{dt} \right ] versus ln[N2O5] using the values determined in step 3.

The gradient and the vertical intercept of the line in the second graph give the values of i and lnk respectively. The differential method is commonly used together with the initial rate method and the isolation method in determining the unknowns of a rate equation with multiple reactants.

 

Next article: Integral method
Previous article: Half-life method
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Rate laws – integral form

An integral rate law mathematically expresses the rate of a reaction in terms of the initial concentration and the measured concentration of one or more reactants over a particular time.

Such a rate law can be derived from its differential form  via simple calculus. Consider the decomposition of hydrogen peroxide to oxygen:

H_2O_2(aq)\rightleftharpoons H_2O(l)+\frac{1}{2}O_2(g)

The rate law is experimentally determined to be first order: rate = k[H2O2]. If we are monitoring the progress of the reaction by measuring the change in concentration of the peroxide, the differential form of the rate law is:

-\frac{d[H_2O_2]}{dt}=k[H_2O_2]\; \; \; \; \; \; \; \; 12

Rearranging and integrating eq12 gives:

\int_{[H_2O_2]_0}^{[H_2O_2]}\frac{1}{[H_2O_2]}d[H_2O_2]=-k\int_{0}^{t}dt

where [H2O2]0 is the concentration of the peroxide at t = 0, i.e. its initial concentration.

We then get:

ln\frac{[H_2O_2]}{[H_2O_2]_0}=-kt\; \; \; or\; \; \; ln[H_2O_2]=-kt+ln[H_2O_2]_0\; \; \; \; \; \; \; \; 13

Eq13 is the integral form of the first order rate law for the decomposition of hydrogen peroxide. The general equation for a species, A, that participates in a first order reaction of vA → B is:

ln\frac{[A]}{[A]_0}=-vkt\; \; \; or\; \; \; ln[A]=-vkt+ln[A]_0\; \; \; \; \; \; \; \; 14

For a zero order reaction, e.g. the decomposition of excess N2O on hot platinum, N_2O\rightarrow N_2+\frac{1}{2}O_2, the rate equation is -\frac{d[N_2O]}{dt}=k. Integrating both sides of this differential rate equation yields:

[N_2O]=-kt+[N_2O]_0\; \; \; \; \; \; \; \; 15

In general, a species, A, that participates in a zero order reaction of vA → B has the equation:

[A]=-vkt+[A]_0\; \; \; \; \; \; \; \; 16

For a second order reaction, e.g.  NO2 + CO → NO + CO2 , the rate equation is:

-\frac{d[NO_2]}{dt}=k[NO_2]^2

and its integral form is:

\frac{1}{[NO_2]}=kt+\frac{1}{[NO_2]_0}\; \; \; \; \; \; \; \; 17

Once again, the generic second order rate equation that involves only one species, A, in a reaction, vA → B, is:

\frac{1}{[A]}=vkt+\frac{1}{[A]_0}\; \; \; \; \; \; \; \; 18

Finally, the diagram below shows the combined concentration-time plot of eq14, eq16 and eq18 for a chemical species A.

 

Next article: Half-life
Previous article: Units of a rate constant
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Integral method (chemical kinetics)

The integral method of determining the rate of a reaction makes use of the integral form of a rate law.

Just like the half-life method and the differential method, the integral method is useful for reactions involving a single reactant, e.g.

N_2O_5(g)\rightleftharpoons 2NO_2(g)+\frac{1}{2}O_2(g)

If the order of the reaction is known, we can determine the value of the rate constant by plotting the appropriate integral rate equations below using experiment data and finding the vertical intercept of the respective linear functions.

Order

 Rate law

Integral rate equation
0 rate=k [A]=-kt+[A]_0
1 rate=k[A] ln[A]=-kt+[A]_0
2 rate=k[A]^2 \frac{1}{[A]}=kt+\frac{1}{[A]_0}

If the order of the reaction is not known, the integral rate equation that gives a straight line with the experiment data is the one that describes the order of the reaction. The integral method can also be used together with the initial rate method and the isolation method in determining the unknowns of a rate equation with multiple reactants.

Next article: Initial rate method
Previous article: Differential method
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Initial rate method (chemical kinetics)

The rate of a reaction decreases with time because the concentrations of reactants decrease as a reaction progresses. This poses a problem when we want to compare reactions under different conditions, e.g. to compare the reaction rates for different concentrations of HCl on CaCO3.

The diagram above shows the pressure of CO2 liberated over time for the reaction of CaCO3 with HCl at three different concentrations: A, B and C. Instead of arbitrarily choosing points on each curve to determine the gradients and hence the respective reaction rates (upper left graph), a basis of comparison must be established before finding the gradients. The initial rate of reaction (i.e. the gradient at t ≈ 0, just after the start of the reaction) is eventually chosen as the reference point (upper right graph), because the concentrations of HCl are approximately the same as that before the start of the respective reactions, especially for slow reactions. It is also chosen partly to minimise the effects of temperature (from exothermic or endothermic reactions) on the system when the reaction progresses. Furthermore, the initial rate of reaction method is useful for studying the forward reaction rate of a reversible reaction where the reverse reaction is negligible at the start. The initial rate method can be used to determine rate equations involving either a single or multiple reactants.

To illustrate the method, consider a constant volume reaction with the rate law:

R=k[A]^i\; \; \; \; \; \; \; \; 25

The experiment is carried out with four different initial concentrations of the reactant, A, with the data plotted in a concentration versus time graph (see diagram below).

Since,

R=\frac{change\, in\, concentration\, of \, reactants\, or\, products}{\, change\, in\, time}

the four gradients of the curves a, b, c and d are the rates of the respective reactions at t = 0, i.e. the initial rates. Taking the natural logarithm of both sides of eq25, we have

lnR=lnk+iln[A]\; \; or\; \; lnR_0=lnk+iln[A]_0\; \; \; \; \; \; \; \; 26

where R0 and [A]0 are the initial rate of reaction and initial concentration of A respectively. If we plot the natural logarithm of the initial reaction rates of the four curves against the natural logarithm of the respective initial concentrations of A, we get a straight line with gradient i and vertical intercept lnk. Therefore, the rate constant and the order of eq25, and hence the entire rate law, can be found.

 

Next article: Why is initial rate proportional to 1/t?
Previous article: Integral method
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Isolation method (chemical kinetics)

Isolation methods are used for reactions with multiple reactants, e.g.

A+B\rightarrow C+D

rate=k\left [ A \right ]^{i} \left [ B \right ]^{j}\; \; \; \; \; \; \; \; 35

There are two isolation methods to determine the rate of a reaction. The first, which is used together with the initial rate method, involves varying the concentration of one of the reactants A, while keeping the concentration of the other reactant B constant. The initial rates of these reactions are then determined. Since the concentration of B is constant for all the experiments and that initial rates are used, eq35 becomes

initial\: rate=k\, '\left [ A \right ]_0^{\: i}\; \; \; \; \; \; \; \; 36

where  k\, '=k\left [ B \right ]_0^{\: j}

By isolating the reactant of interest, A, eq35 has changed from an (i + j) order equation to a pseudo-i order equation. Taking the natural logarithm of both sides of eq36 and plotting the experimental results in a ln(initial rate) versus ln[A]0 graph, we can find the gradient of the curve, which is the order with respect to A, and the vertical intercept of the curve, which corresponds to ln(k[B]0 j). To find j and hence the value of k, we repeat the series of experiments by varying concentrations of B while keeping the concentration of A constant, and carrying out the same graphical analysis as before.

The second isolation method involves using an excess amount of one reactant, e.g. B, such that its concentration remains unchanged during the prolonged course of the reaction. Eq35 becomes

rate=k''\left [ A \right ]^{i}\; \; \; \; \; \; \; \; 37

ln\left ( rate \right )=iln\left [ A \right ]+lnk''\; \; \; \; \; \; \; \; 38

where k''=k\left [ B \right ]^{j}

With just a single experiment, the gradients at various points on the curve of a [A] versus time graph correspond to the reaction rates at different [A]. These data are then used to construct another graph with eq38 to determine i and lnk”. Similarly, to find k and j, we repeat the experiment, this time with [A] in excess and carry out the same graphical analysis as before.

 

Question

Can the first isolation method be used without the initial rate method, i.e. can we, with the first isolation method, let the reaction run its course as per the situation in eq37?

Answer

No. This is because the concentration of the reactant that is kept constant is not in excess. The concentration of that reactant will change during the course of the reaction, rendering k” a variable. In other words, the concentration of the reactant that is kept constant in the first method is only constant during the duration necessary for the initial rate of the reaction to be taken.

 

 

Next article: Arrhenius equation
Previous article: Why is Initial rate proportional to 1/t?
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Why is initial rate proportional to 1/t?

The ‘initial rate proportional to 1/t’ concept is applicable to a chemical kinetics experiment that has the initial concentration of a reactant varied but the measured amount of a product fixed. One such experiment is the decomposition of hydrogen peroxide over a platinum catalyst, while another is the iodine clock. For the decomposition experiment, we have:

2H_2O_2(aq)\rightleftharpoons2H_2O(l)+O_2(g)

Using various initial concentrations of H2O2, different times taken to collect a fixed volume of oxygen are recorded. The diagram below illustrates the setup, where the fixed volume of oxygen produced under constant temperature is measured by a fixed change in pressure of the constant-volume system.

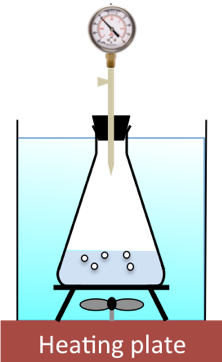
Since the reaction is very slow, we assume that the initial concentration of H2O2 for each experiment remains relatively unchanged for the volume of oxygen generated (the change in pressure of the system can be fixed at an amount that does not exceed three minutes to occur). Using eq10, and assuming gases behave ideally, we can write

initial\, rate=\frac{d[O_2]}{dt}=\frac{\Delta (n_{O_2}/V)}{\Delta t}=\frac{\Delta p}{RT\Delta t}\; \; \; \; \; \; \;\; 27

To produce a fixed volume of oxygen, the change in amount of oxygen, and hence the change in pressure of the system, is constant regardless of the concentration of H2O2 used. Thus,

initial\, rate=C\frac{1}{\Delta t}\; \; \; \; \; \; \; \; 28

where C is a constant and is equal to \frac{\Delta p}{RT}.

This answers the question of why initial rate is proportional to 1/t.

To develop an equation that that allows us to further analyse the decomposition reaction, we propose the following rate law:

initial\, rate=k[H_2O_2]_0^{\;\: i}\; \; \; \; \; \; \; \; 29

where [H2O2]0 is the initial concentration of H2O2.

Taking the natural logarithm for both sides of eq28 and eq29, we have

ln(initial\, rate)=ln\frac{1}{\Delta t}+ln\frac{\Delta p}{RT}\; \; \; \; \; \; \; \; 30

and

ln(initial\, rate)=iln[H_2O_2]_0+lnk\; \; \; \; \; \; \; \; 31

Substitute eq31 in eq30

ln\frac{1}{\Delta t}=iln[H_2O_2]_0+ln\frac{k}{\Delta p/RT}\; \; \; \; \; \; \; \; 32

Therefore, using the time measurements for the fixed change in pressure to occur for different initial concentrations of H2O2, a plot of ln\frac{1}{\Delta t} versus ln[H_2O_2]_0  gives a gradient of the order of the reaction, i, and a vertical intercept of ln\frac{k}{\Delta p/RT}  where k is the rate constant.

Question

Eq32 is derived using the rate equation \frac{d[O_2]}{dt}=k[H_2O_2]_0^{\; \, i}. What if we define the rate equation as -\frac{1}{2}\frac{d[H_2O_2]}{dt}=k_1[H_2O_2]_0^{\; \, i} ?

Answer

-\frac{1}{2}\frac{\Delta n_{H_2O_2}/V_{H_2O_2}}{\Delta t}=k_1[H_2O_2]_0^{\: \, i}

ln\left ( -\frac{1}{2}\frac{\Delta n_{H_2O_2}}{V_{H_2O_2}} \right )+ln\frac{1}{\Delta t}=lnk_1+iln[H_2O_2]_0

ln\frac{1}{\Delta t}=iln[H_2O_2]_0+ln\left ( \frac{k_1}{-\Delta n_{H_2O_2}/2V_{H_2O_2}} \right )\; \; \; \; \; \; \; \; 33

To produce a fixed volume of oxygen, the change in amount of H2O2, \Delta n_{H_2O_2}, is a constant value regardless of the initial amounts of H2O2. For example, to produce 1 mole of oxygen, the change in amount of H2O2 is always -2 moles irrespective of how many moles of H2O2 there are to begin with. Furthermore, the same volume of H2O2 is used as we vary [H2O2]. So, the 2nd term on RHS of eq33 is a constant, which makes eq33, like eq32, a linear function.

Comparing eq33 with eq32,

k_1=-\frac{\Delta n_{H_2O_2}RT}{2V_{H_2O_2}\Delta p}k

 

Next article: Isolation method
Previous article: Initial rate method
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Arrhenius equation (chemical kinetics)

The Arrhenius equation was conceived by Svante Arrhenius, a Swedish chemist, in 1889.

It relates the rate constant, k, of a reaction with the temperature of the reaction, T, as follows:

k=Ae^{-\frac{E_a}{RT}}\; \; \; \; \; \; \; \; 39

where Ea is the activation energy of the reaction, R is the universal gas constant and A is the pre-exponential factor. The values of Ea and A of a reaction are experimentally determined.

The Arrhenius equation is based on the van’t Hoff equation: \Delta_rH^o=RT^2\frac{dlnK}{dT}. Consider a reversible elementary reaction A+B\; \; \begin{matrix} k_1\\\rightleftharpoons \\ k_2 \end{matrix}\; \; P, where k1 and k2 are the rate constants of the forward and reverse reactions respectively. At equilibrium, rate_1=rate_2 and therefore, k_1[A][B]=k_2[P] or \frac{k_1}{k_2}=\frac{[P]}{[A][B]}=K. Substituting K=\frac{k_1}{k_2} in the van’t Hoff equation,

\Delta_rH^o=RT^2\frac{dlnk_1}{dT}-RT^2\frac{dlnk_2}{dT}

If we define RT^2\frac{dlnk}{dT}=E_a,

\Delta_rH^o=E_{a1}-E_{a2}\; \; \; \; \; \; \; \; 40

Eq40 is best interpreted using a potential energy graph:

The definition of activation energy, E_a=RT^2\frac{dlnk}{dT}, results in eq39 when integrated. Taking the natural logarithm on both sides of eq39,

lnk=lnA-\frac{E_a}{RT}\; \; \; \; \; \; \; \; 41

Eq41 is a linear function with dependent variable lnk and independent variable \frac{1}{T}, so that a plot of  lnk versus \frac{1}{T} gives a gradient of -\frac{E_a}{R} and vertical intercept of lnA.

 

Question

Are the activation energy Ea and pre-exponential factor A of a reaction independent of temperature?

Answer

For the Arrhenius equation to be applicable, a plot of lnk versus 1/T must, with strong linear correlation, produce a straight line when values of k at various T are substituted in eq41. This implies that the activation energy Ea and pre-exponential factor A of a reaction are constants and therefore independent of temperature. In fact, the Arrhenius equation works reasonably well for many reactions over a temperature range of about 100 K. However, deviations from the equation do occur for some other reactions.

A more rigorous approach to analyse the relation between k and T using the transition state theory (TST) reveals the temperature-dependence of the activation energy of a reaction, with E_a=\Delta^{\ddagger}H^o+xRT, where x = 1 for unimolecular gas-phase reactions and x = 2 for bimolecular gas-phase reactions. The TST also shows that the pre-exponential factor is dependent on temperature, where A=\frac{\kappa e^xkRT}{p^oh}^2e^{\frac{\Delta^{\ddagger}S^o}{R}}.

So why does the Arrhenius equation work for so many reactions when both the activation energy and pre-exponential factor of a reaction are temperature-dependent? For Ea, the value \Delta^{\ddagger}H^o is usually much bigger than xRT, and for A, T2 is dwarfed by the term \frac{\kappa e^xkR}{p^oh}e^{\frac{\Delta^{\ddagger}S^o}{R}}.

 

 

Next article: REaction mechanism
Previous article: Isolation method
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Posted on

Iodine clock (chemical kinetics)

The iodine clock is a chemical clock experiment devised by Hans Landolt, a Swiss chemist, in 1886. It illustrates the theories of chemical kinetics and redox chemistry via reactions that generate aqueous iodine as a product, and manifests the concept of a chemical clock through the time taken by one or more parallel reactions to consume the iodine produced.

An example is the oxidation of iodide by hydrogen peroxide to form aqueous iodine:

H_2O_2+2H^++2I^-\rightarrow 2H_2O+I_2\; \; \; \; \; \; \; \; 46

The iodine produced immediately reacts with a known amount of reducing agent, e.g. sodium thiosulphate, which is added to the peroxide-iodide mixture together with some starch solution at the start of the reaction.

2S_2O_3^{\; \: 2-}+I_2\rightarrow S_4O_6^{\; \: 2-}+2I^-\; \; \; \; \; \; \; \; 47

As the thiosulphate-iodine reaction occurs at a much faster rate than the peroxide-iodide reaction and it regenerates the exact stoichiometric amount of iodide ions that is present at the start of the reaction, the presence of iodine is only detected when all of the thiosulphate has been reacted.

When there is no more thiosulphate to remove the iodine, iodine combines with the unreacted iodide to form the triiodide ion, which in turn forms an intense blue-black charge-transfer complex with starch:

I_2+I^-\rightleftharpoons I_3^{\; \; -}\; \; \begin{matrix} starch\\\rightarrow \end{matrix}\; \; coloured\, complex

The different times needed for the mixtures to turn blue-black are recorded for a series of experiments using different concentrations of hydrogen peroxide, acid and iodide. For a constant amount of thiosulphate, the longer the time taken for the mixture to turn blue-black, the slower the peroxide-iodide reaction. In other words, the rate of the peroxide-iodide reaction is inversely proportional to the time taken for the mixture to turn blue-black.

Another version of the iodine clock experiment is the reaction between ammonium persulphate and potassium iodide:

S_2O_8^{\; \; 2-}+2I^-\rightarrow 2SO_4^{\; \; 2-}+I_2

I_2+2S_2O_3^{\; \; 2-}\rightarrow2I^-+S_4O_6^{\; \; 2-}

 

Next article: Iodine clock experiment
Previous article: Reaction mechanism
Content page of intermediate chemical kinetics
Content page of intermediate chemistry
Main content page
Mono Quiz