Rate laws (chemical kinetics)

The rate of a reaction has been defined in a basic level article as:

For a simple reaction, A → B at constant volume V₁, we can define its rate as

where n_B is the amount of B.

Since the rate of formation of product must be the same as the rate of consumption of the reactant, and that the rate of a reaction is defined as a positive value, we have:  . 

Suppose we have another reaction, C → D at a different constant volume V₂, with a rate:

To have a meaningful comparison of the rates of these two reactions with different reacting volumes, we need a common basis, which can be obtained by dividing eq2 and eq3 by their respective volumes. Therefore, a better definition of the rate of a reaction is:

Consider an experiment where HCl is added to CaCO₃ to produce CO₂ in a rigid vessel with a pressure gauge. The data collected are presented in a CO₂ pressure versus time plot. If we use a constant mass of CaCO₃ and 3 different concentrations of 20 cm³ of HCl, we have 3 different gradients at the origin, which represent 3 initial rates of reaction (see diagram below) with R_A corresponding to the reaction with the highest concentration of HCl and R_C relating to the reaction with the lowest concentration of HCl.

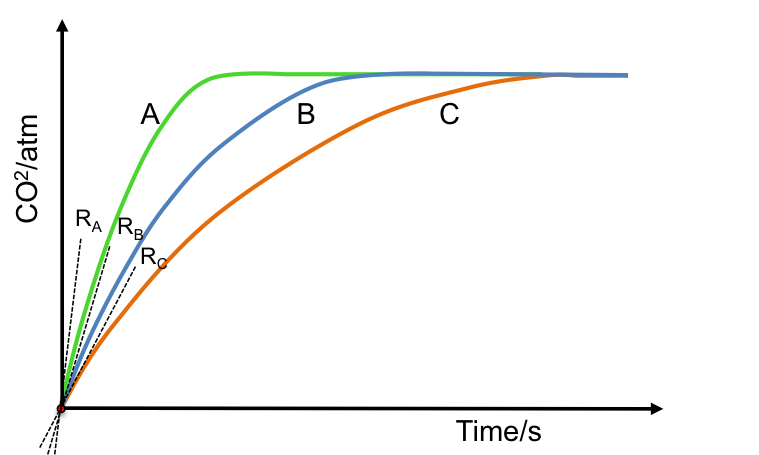
The above results imply that the rate of reaction is proportional to the concentration of the reactant used. Therefore, in addition to eq4, we can also expressed the rate of a reaction in the form of an equation known as a rate law:

where [H₃O⁺] is the concentration of hydroxonium ions from HCl and k is a proportionality constant called the rate constant. Combining eq4 and eq5,

Eq6 means that an increase in concentration of hydroxonium ions increases the rate of change in concentration of CO₂, which is measured by the rate of change in pressure of CO₂, since .

 

Next article: Rate laws – differential form

Content page of intermediate chemical kinetics

Content page of intermediate chemistry

Main content page