The electronic molecular partition function is a measure of the number of thermally accessible electronic energy states available to a single non-interacting molecule at a specific temperature.
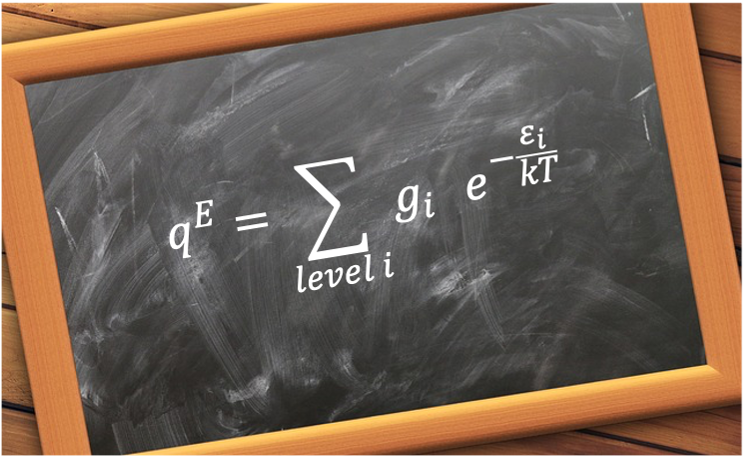
It is defined by eq255:
where
is the degeneracy of the
-th electronic level,
is the energy of the
-th electronic state,
is the Boltzmann constant,
is the absolute temperature.
Expanding the above equation yields:
where the ground electronic energy level, , is the lowest electronic energy level with rotational quantum number
and vibrational quantum number
.
For many diatomic molecules under standard laboratory conditions (e.g. room temperature), the electronic partition function simplifies significantly. This is because the energy gap between the ground state and the first excited electronic state is often much larger than , leading to an exponentially small population in the excited states. In other words,
for
at temperatures up to 10000 K, giving:
Since the ground electronic level for most diatomic molecules, as well as monatomic species with filled subshells, is nondegenerate, .
Some exceptions to this generalisation include O2 and NO. The ground electronic level of O2 consists of two unpaired electrons, each occupying one of two degenerate antibonding molecular orbitals, resulting in a triplet state. Therefore, . Furthermore, O2 has an excited electronic state that becomes significantly populated above 1500 K, so
at higher temperatures.
In its ground electronic state, NO has a single unpaired electron occupying one of two degenerate antibonding molecular orbitals. These orbitals are formed by the overlap of the
and
atomic orbitals of N and O. Consequently, the unpaired electron can have an orbital angular momentum projection of either +1 or -1, giving rise to two degenerate orbital states. Additionally, the unpaired electron is characterised by a doublet state (spin degeneracy of 2). Due to spin-orbit coupling, each of the two orbital states is further split into two fine-structure levels, with a small energy separation of approximately 0.015 eV (or 121 cm-1). Therefore,
at
, and it rapidly approaches 4 as the temperature increases.
Since the electronic partition function is tied directly to electronic energy levels, it reflects the electronic structure of the molecule. Spectroscopic data from techniques such as UV-Vis spectroscopy or photoelectron spectroscopy provide the necessary input for estimating the energy levels , and hence computing
. Self-consistency methods can also be used to numerically evaluate
with accuracy, especially in systems where experimental
data are lacking.
In practice, becomes crucial in systems where excited electronic states are thermally accessible, such as:
-
- High-temperature systems (e.g. combustion, plasma),
- Photochemically excited molecules,
- Transition metals and radicals, which often have low-lying excited states,
- Astrophysical and atmospheric systems where thermal populations can include excited states.
In these cases, the electronic partition function influences calculations of internal energy, entropy, heat capacity and equilibrium constants.